
题目列表(包括答案和解析)

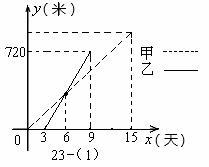
(1) A、B两村之间的公路进行对接修筑,甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图23-(1)是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
①乙工程队每天修公路多少米?
②分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式;
③若乙工程队后来进入施工后,不提前离开,直到公路对接完工,那么施工过程共需几天?

(2)如图23-(2),直线![]() 分别与x轴、y轴交于点A、B,在第一象限取点C,使△ABC成为等腰直角三角形;如果在第二象限内有一点P(a,
分别与x轴、y轴交于点A、B,在第一象限取点C,使△ABC成为等腰直角三角形;如果在第二象限内有一点P(a,![]() ),使△ABP的面积与Rt△ABC的面积相等,求a的值.
),使△ABP的面积与Rt△ABC的面积相等,求a的值.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com