
题目列表(包括答案和解析)
(06年北京卷理)已知 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
已知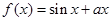 是
是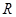 上的增函数,则实数
上的增函数,则实数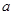 的取值范围是
的取值范围是
已知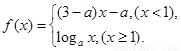 是
是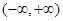 上的增函数,那么实数a的取值范围是( )
上的增函数,那么实数a的取值范围是( )
A.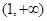 B.
B.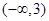 C.
C. 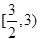 D.
D.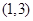
已知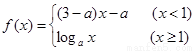 是
是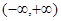 上的增函数,那么a的取值范围是 ……………………………( )
上的增函数,那么a的取值范围是 ……………………………( )
(A) (1,+∞) ; (B) (0,3); (C) (1,3); (D) [ ,3).
,3).
已知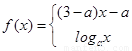
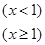 是(-∞,+∞)上的增函数,则a的取值范围是( ).
是(-∞,+∞)上的增函数,则a的取值范围是( ).
A.(1,+∞) B.
(1,3) C.
[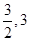 ) D.
(1,
) D.
(1, 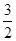 )
)
一、选择题:本大题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
理
A
C
B
D
A
C
B
C
C
B
B
D
文
D
C
B
D
B
C
B
C
C
B
A
D
二、填空题:本大题共4小题,每小题5分,共20分
13.(理)2 (文) 14.(理) (文)243 15. 16.(1,2)(2,3)
三、解答题:本大题共6小题,共70分.
17.解: ????????????????????????????????????????????????????????? (2分)
由正弦定理得???????????????????????????????????????????? (4分)
??????????????????????????????????????????????????????????????? (5分)
??????????????????????????????????????????????? (6分)
???????????????????????????????????????????????????? (8分)
???????????????????????????????????????????????????????????????????????????????????????? (9分)
????????????????????????????????????????????????????????????????? (10分)
18.(理)解:????????????????????????????????????????? (2分)
??????????????????????????????????????????????????????????????????????????????????????????????????????????????? (4分)
????????????????????????????????????????? (6分)
??????????????????????????????????????????????????????????????????????????????????????????????? (8分)
由此可知,,从而两厂材料的抗拉强度指数平均水平相同,但甲厂材料相对稳定,该选甲厂的材料。??????????????????????????????????????????????????????????????????????????????????????????????? (12分)
(文)解:记“甲第次试跳成功“为事件,“乙第次试跳成功”为事件,依题意得且相互独立?????????????????????????????????????????????????????????????? (2分)
(I)“甲第三次试跳才成功”为事件,且三次试跳相互独立,
。
答:甲第三次试跳才成功的概率为0.063????????????????????????????????????????? (6分)
(Ⅱ)“甲、乙两人在第一次试跳中至少有一人成功”为事件,
解法一:且彼此互斥,
?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? (8分)
????????????????????????????????????????????????????????????????????????? (12分)
解法二:
答:甲、乙两人在第一次试跳中至少有一人成功的概率为0.88
19.(I)证明:由直三棱柱性质知
又
???? …………………………………(理4分文6分)
(Ⅱ)以A为原点,分别为
轴,建立如图的空间直角坐标系
直线
连结易知是平面的一个法向量,
=(0,1,-1),设为平面
的一个法向量,则
又
令得得
设二面角的大小为,则
二面角的大小为…………………………(理8分文12分)
(Ⅲ)又
点到平面的距离………………………(理12分)
20.(理)解:(I)
当,即时,在上单调递增
???????????????????????????????????? (2分)
??????????????????????????????? (4分)
?????????????????????????????????????????????????? (6分)
(Ⅱ)令
??????????? (7分)
??????????? (10分)
??????????????????????????????????????????????????????????????????????????????????????????????????????????????? (12分)
(文)解:(I)因为边所在直线的方程为
…………………………………(1分)
…………………………(4分)
(Ⅱ)由??????????????????????????? (5分)
????????????????????????????????????????????????? (6分)
???????????????????????????? (8分)
(Ⅲ)因为动圆过点,所以是该圆的半径,又因为动圆与圆外切,
所以,
即
故点的轨迹是以为焦点,实轴长为的双曲线的左支。
因为实半轴长半焦距
所以虚半轴长
从而动圆的圆心的轨迹方程为????????????????????????? (12分)
21.(理)
解法一:(I)如图,设把代入得
,由韦达定理得???????????????????????? (2分)
点的坐标为???????????????????????????????? (3分)
设抛物线在点处的切线的方程为
将代入上式得
(Ⅱ)
由(I)知
???????????????????? (9分)
??????????????????? (11分)
?????????????????????????????????????????????????????????????????? (12分)
解法二:(I)设
??????????????????????? (2分)
????????????????????????????????????????????????????????????????????????????????????????????????????????????? (4分)
????????????????????? (6分)
(Ⅱ)
由(I)知
则
???????????????????????????????????????????????????????????????????????????????????? (10分)
??????????????????????????????????????????????????????????????????? (12分)
(文)解:(I)
?????????????????????????????????????????????????????????? (3分)
由于,故当时达到其最小值,即
??????????????????????????????????????????????????????????????????????????????? (6分)
(Ⅱ)
列表如下:
+
0
-
0
+
极大值
极小值
??????????????????????????????????????????????????????????????????????????????????????????????????????????????? (10分)
由此可见,在区间和单调增加,在区间单调减小,
极小值为极大值为?????????????????????????????????????????????? (12分)
22. 解:
(I)????????????????????????????????????????????????? (2分)
(Ⅱ)由(I)知
……
???????????????????????????????????????????? (5分)
????????????????????????????????????????????????????????? (8分)
(文)(Ⅲ)
???????????????????????????????????????????????????????? (12分)
(理)(Ⅲ)
?????????????????????????????????? (12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com