题目列表(包括答案和解析)
（07。上海物理卷）如图（a）所示，光滑的平行长直金属导轨置于水平面内，间距为L、导轨左端接有阻值为R的电阻，质量为m的导体棒垂直跨接在导轨上。导轨和导体棒的电阻均不计，且接触良好。在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场，磁感应强度大小为B。开始时，导体棒静止于磁场区域的右端，当磁场以速度v1匀速向右移动时，导体棒随之开始运动，同时受到水平向左、大小为f的恒定阻力，并很快达到恒定速度，此时导体棒仍处于磁场区域内。
（1）求导体棒所达到的恒定速度v2；
（2）为使导体棒能随磁场运动，阻力最大不能超过多少？
（3）导体棒以恒定速度运动时，单位时间内克服阻力所做的功和电路中消耗的电功率各为多大？
（4）若t＝0时磁场由静止开始水平向右做匀加速直线运动，经过较短时间后，导体棒也做匀加速直线运动，其v-t关系如图（b）所示，已知在时刻t导体棒瞬时速度大小为vt，求导体棒做匀加速直线运动时的加速度大小。
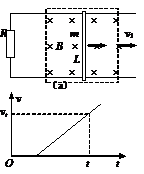（07。上海物理卷）如图（a）所示，光滑的平行长直金属导轨置于水平面内，间距为L、导轨左端接有阻值为R的电阻，质量为m的导体棒垂直跨接在导轨上。导轨和导体棒的电阻均不计，且接触良好。在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场，磁感应强度大小为B。开始时，导体棒静止于磁场区域的右端，当磁场以速度v1匀速向右移动时，导体棒随之开始运动，同时受到水平向左、大小为f的恒定阻力，并很快达到恒定速度，此时导体棒仍处于磁场区域内。
（1）求导体棒所达到的恒定速度v2；
（2）为使导体棒能随磁场运动，阻力最大不能超过多少？
（3）导体棒以恒定速度运动时，单位时间内克服阻力所做的功和电路中消耗的电功率各为多大？
（4）若t＝0时磁场由静止开始水平向右做匀加速直线运动，经过较短时间后，导体棒也做匀加速直线运动，其v-t关系如图（b）所示，已知在时刻t导体棒瞬时速度大小为vt，求导体棒做匀加速直线运动时的加速度大小。
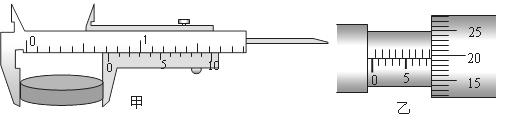
图中；游标卡尺的示数是 mm。螺旋测微器的示数是 mm。
；
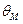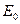且完全转化为两小球动能，求从爆炸到发生第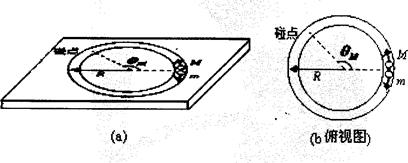
[来源:Z。xx。k.Com]
如图所示，半径R＝0.9 m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点B与长为l＝l m的水平面相切于B点，BC离地面高h＝0.45 m，C点与一倾角为θ＝30??的光滑斜面连接。质量m＝1.0 kg的小滑块从圆弧顶点D由静止释放，已知滑块与水平面间的动摩擦因数μ＝0.1，取g＝10 m／s2。求：
（1）小滑块刚到达圆弧的B点时对圆弧的压力；
（2）小滑块从C点运动到地面所需的时间。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
C
ACD
D
A
B
D
BCD
ACD
BD
AC
13.(1) ①从该时刻经
，质点M恰经过平衡位置，所以位移为0。②该时刻。振动增强的点是：M、O、P、Q；振动减弱的点是：N。 (2) C
14．（10分）（1）a.干电池正常；b.电键正常；c.闭合天关关回路是连通的，没有断路之处。（3分）（每答对一点得1分）；
（2）ACF（3分） （有一处错误即不给分）
（3）由于灯丝的电阻率随温度的升高而增大，欧姆表测出的小灯泡电阻值是常温下的电阻值，而根据公式计算出的小灯泡电阻值是高温下（正常工作）的电阻值。（3分，每答对一点得1分） （4）H（3分）
15. （10分）（1）刻度尺; （1分）
（2）把木板的末端垫起适当高度
以平衡摩擦力 （2分）
（3）点距均匀(1分)
（4）2W、3W、4W、5W(2分)
（5）v2（1分）；图像 (2分)
（6）分析误差来源或改进试验
方案或测量手段，重新进行试验（1分）；
若答：“修改试验数据数据，
使之符合自己的推测”得0分；
16.（1）分析：要求了解光电效应的规律及光子说理论。
解答：由爱因斯坦光电效应方程可得：
=W+
m
∴=1.9+1.0=2.9eV=2.9×1.6×10―19J
∴λ=
=4.3×10―7 m
(2)评析:（1） 输电线的电阻为：
①
P损=P1×4% ②
P损=I2 R ③
P2=P1 ④
P2=I2U2 ⑤
由①②③④⑤式得升压变压器的输出电压：U2=80000V ⑥
(2) 输电线上的电压的损失：U损=I2R=3200V ⑦
17．（14分）分析和解：（1）带电粒子经过电场加速，进入偏转磁场时速度为v，由动能定理
…………………①（1分）
进入磁场后带电粒子做匀速圆周运动，轨道半径为r
………………②（2分）
打到H点有 
………………………③（1分）
由①②③得 
…………(1分)
（2）要保证所有粒子都不能打到MN边界上，粒子在磁场中运动偏角小于90°，临界状态为90°，如图所示，磁场区半径
（2分）
所以磁场区域半径满足
（1分）
18．(14分) 解：（1）设小球经过B点时的速度大小为vB，由机械能守恒得：
（1分）
求得：vB=10m/s. （1分）
（2）设小球经过C点时的速度为vC，对轨道的压力为N，则轨道对小球的压力N’=N，根据牛顿第二定律可得：
N’－mg = 
（2分）
由机械能守恒得：
（2分）
由以上两式及N’= N求得：N = 43N. （2分）
（3）设小球受到的阻力为f，到达S点的速度为vS，在此过程中阻力所做的功为W，易知vD= vB，由动能定理可得：
（2分）
求得W=－68J. （2分）
小球从D点抛出后在阻力场区域内的运动轨迹不是抛物线．（2分）
19.（16分） （1）由题意可知：板1为正极，板2为负极 ①
两板间的电压U＝
②
而：S＝πr2 ③
带电液滴受的电场力：F＝qE=
④
故：F－mg＝－mg＝ma
a=
－g
⑤
讨论：
一．若 a>0
液滴向上偏转，做类似平抛运动
y＝ 
⑥
当液滴刚好能射出时：
有 l＝v0t t＝
y＝d
故 d=
⑦
由②③⑦得 K1＝ 
⑧
要使液滴能射出，必须满足 y<d 故 K＜K1
二．若 a＝0
液滴不发生偏转，做匀速直线运动，此时 a=
－g＝0 ⑨
由②③⑨得 K2＝
⑩
液滴能射出，必须满足K＝K2
三．若 a<0,、，液滴将被吸附在板2上。
综上所述：液滴能射出，
|
替代⑧式中的d
12
13
⑴木块和木盒分别做匀减速运动，加速度大小分别为：aA = μAg = 
代入数据得：T = 2s
（2分）
SA= vA T1－
代入数据得；T1=T=2s （2分）
m/s 
m/s 
m/s