
题目列表(包括答案和解析)
 组成的图案和算式,解答问题:
组成的图案和算式,解答问题:

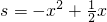 (x>0),利用函数的图象或通过配方均可求得该函数的最大值.
(x>0),利用函数的图象或通过配方均可求得该函数的最大值.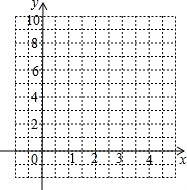
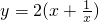 (x>0),问题就转化为研究该函数的最大(小)值了.
(x>0),问题就转化为研究该函数的最大(小)值了.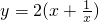 (x>0)的最大(小)值.
(x>0)的最大(小)值.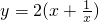 (x>0)的图象:
(x>0)的图象:| x | … | 1/4 | 1/3 | 1/2 | 1 | 2 | 3 | 4 | … |
| y | … | 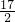 |  | 5 | 4 | 5 |  | 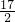 | … |
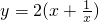 (x>0)有最______值(填“大”或“小”),是______.
(x>0)有最______值(填“大”或“小”),是______.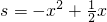 (x>0)的最大值,请你尝试通过配方求函数
(x>0)的最大值,请你尝试通过配方求函数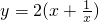 (x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,
(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,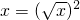 〕
〕 ,以BC边所在直线为x轴,BC边上的高线AO所在的直线为y轴建立平面直角坐标系.
,以BC边所在直线为x轴,BC边上的高线AO所在的直线为y轴建立平面直角坐标系.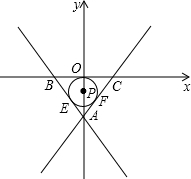
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com