(2)设函数的图象与的图象有交点.证明: 【查看更多】

设函数f（x）=x²-mlnx，h（x）=x²-x+a．
（1）当a=0时，f（x）≥h（x）在（1，+∞）上恒成立，求实数m的取值范围；
（2）当m=2时，若函数k（x）=f（x）-h（x）在[1，3]上恰有两个不同零点，求实数 a的取值范围；
（3）当m=2时，如果函数g（x）=-f（x）-ax的图象与x轴交于两点A（x₁，0）、B（x₂，0）且0＜x₁＜x₂．求证：g′（px₁+qx₂）＜0（其中正常数p，q满足p+q=1，且q≥p）．

已知函数的图象是自原点出发的一条折线．当时，该图象是斜率为的线段（其中正常数），设数列由定义．求：

求和的表达式；

求的表达式，并写出其定义域；

证明：的图像与的图象没有横坐标大于1的交点．

查看答案和解析>>

设函数f（x）=ax+

（a，b∈Z），曲线y=f（x）在点（2，f（2））处的切线方程为y=3．
（Ⅰ）求f（x）的解析式，并判断函数y=f（x）的图象是否为中心对称图形？若是，请求其对称中心；否则说明理由．
（II）证明：曲线y=f（x）上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值．
（III）将函数y=f（x）的图象向左平移一个单位后与抛物线y=ax²（a为非0常数）的图象有几个交点？（说明理由）

查看答案和解析>>

设函数f（x）= $数学公式$ + $数学公式$ ，
（1）求函数f（x）的定义域；
（2）判断函数f（x）的单调性，并给出证明；
（3）已知函数f（x）的反函数f^-1（x），问函数y=f^-1（x）的图象与x轴有交点吗？若有，求出交点坐标；若无交点，说明理由．

查看答案和解析>>

设函数f（x）=x²-mlnx，h（x）=x²-x+a．
（1）当a=0时，f（x）≥h（x）在（1，+∞）上恒成立，求实数m的取值范围；
（2）当m=2时，若函数k（x）=f（x）-h（x）在[1，3]上恰有两个不同零点，求实数 a的取值范围；
（3）当m=2时，如果函数g（x）=-f（x）-ax的图象与x轴交于两点A（x₁，0）、B（x₂，0）且0＜x₁＜x₂．求证：g′（px₁+qx₂）＜0（其中正常数p，q满足p+q=1，且q≥p）．

查看答案和解析>>

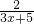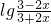一、选择题

CCCBB BBDAB CA

二、填空题

13、 14、2 15、 16、③④