【老题重现】
求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.
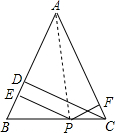
已知:△ABC中,AB=AC,点P是BC边上任意一点,PE⊥AB于E,PF⊥AC于F,CD是AB边上的高线.
求证:PE+PF=CD
证明:连接AP,
∵S
△ABP+S
△ACP=S
△ABC∴
+=∵AB=AC
∴PE+PF=CD
【变式应用】
请利用“类比”和“化归”两种方法解答下面问题:
求证:等边三角形内上任意一点到三边的距离和等于一边上的高.
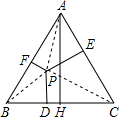
已知:点P是等边△ABC内任意一点,PD⊥BC于D,PE⊥AC于E,PF⊥AB于F,AH是BC边上的高线.
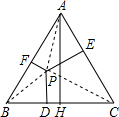
求证:PD+PE+PF=AH
证明:
方法(一)类比:通过类比上题的思路和方法,模仿上题的“面积法”解决本题.
连接AP,BP,CP
方法(二)化归:如图,通过MN在等边△ABC中构造符合“老题”规律的等边△AMN,化“新题”为“老题”,直接利用“老题重现”的结论解决问题.
过点P作MN∥BC,交AB于M,交AC于N,交AH于G.
【提炼运用】
已知:点P是等边△ABC内任意一点,设到三边的距离分别为a、b、c,且使得以a、b、c为边能够构成三角形.
请在图中画出满足条件的点P一切可能的位置,并对这些位置加以说明.

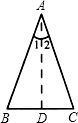 “等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.
“等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸. “等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.
“等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.
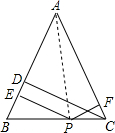 求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.
求证:等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.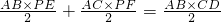
 【老题重现】
【老题重现】
