
题目列表(包括答案和解析)
、有如图(表1)所示的3行5列的数表,其中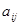 表示第
表示第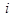 行第
行第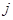 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列 。规则如下:(1)先取出
。规则如下:(1)先取出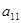 ,并记
,并记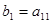 ;若
;若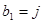 ,则从第
,则从第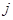 列取出行号最小的数字,并记作
列取出行号最小的数字,并记作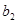 ;(2)以此类推,当
;(2)以此类推,当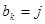 时,就从第
时,就从第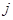 列取出现存行号最小的那个数记作
列取出现存行号最小的那个数记作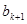 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列 :1,2,4,5,3,2,5,1,3,1. 试问数列
:1,2,4,5,3,2,5,1,3,1. 试问数列 的项数恰为15的概率为
。
的项数恰为15的概率为
。
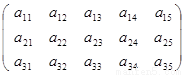
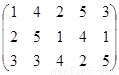
(表1) ( 表2)
、有如图(表1)所示的3行5列的数表,其中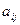 表示第
表示第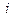 行第
行第 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列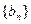 。规则如下:(1)先取出
。规则如下:(1)先取出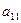 ,并记
,并记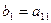 ;若
;若 ,则从第
,则从第 列取出行号最小的数字,并记作
列取出行号最小的数字,并记作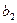 ;(2)以此类推,当
;(2)以此类推,当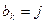 时,就从第
时,就从第 列取出现存行号最小的那个数记作
列取出现存行号最小的那个数记作 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列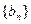 :1,2,4
:1,2,4 ,5,3,2,5,1,3,1. 试问数列
,5,3,2,5,1,3,1. 试问数列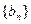 的项数恰为15的概率为 。
的项数恰为15的概率为 。
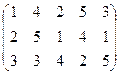
(表1) ( 表2)
 表示第
表示第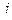 行第
行第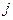 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列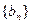 。规则如下:(1)先取出
。规则如下:(1)先取出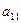 ,并记
,并记 ;若
;若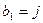 ,则从第
,则从第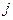 列取出行号最小的数字,并记作
列取出行号最小的数字,并记作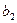 ;(2)以此类推,当
;(2)以此类推,当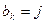 时,就从第
时,就从第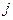 列取出现存行号最小的那个数记作
列取出现存行号最小的那个数记作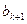 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列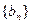 :1,2,4
:1,2,4 ,5,3,2,5,1,3,1. 试问数列
,5,3,2,5,1,3,1. 试问数列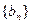 的项数恰为15的概率为 。
的项数恰为15的概率为 。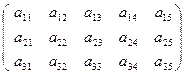
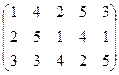
已知函数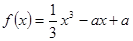
(Ⅰ)若函数 恰好有两个不同的零点,求
恰好有两个不同的零点,求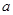 的值。
的值。
(Ⅱ)若函数 的图象与直线
的图象与直线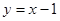 相切,求
相切,求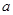 的值及相应的切点坐标。
的值及相应的切点坐标。
【解析】第一问中,利用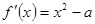
当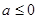 时,
时, 在
在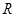 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当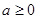 时,
时,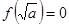 或
或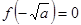 ,得
,得
第二问中,设切点为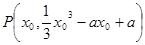 ,则
,则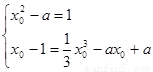
所以,当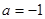 时,
时,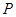 为
为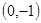 ;当
;当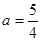 时,
时,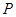 为
为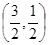
解:(Ⅰ)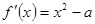 2分
2分
当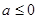 时,
时, 在
在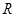 单调递增,此时
单调递增,此时 只有一个零点;
只有一个零点;
当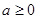 时,
时,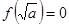 或
或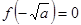 ,得
,得 4分
4分
(Ⅱ)设切点为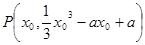 ,则
,则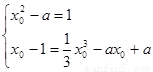 3分
3分
所以,当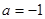 时,
时,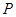 为
为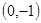 ;当
;当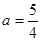 时,
时,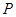 为
为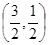
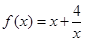 ,
, 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下: | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
 | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
 值随
值随 值变化的特点,完成下列问题:
值变化的特点,完成下列问题: 时,
时,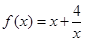 在区间
在区间 上递减,在区间 上递增;
上递减,在区间 上递增; = 时,
= 时,  取到最小值为 ;
取到最小值为 ; 时,
时,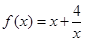 有最 值为 ,此时
有最 值为 ,此时 = ;
= ;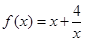 在区间
在区间 上递减;
上递减; 在
在 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数 的取值范围。
的取值范围。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com