
题目列表(包括答案和解析)
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 9 | 12 | 5 | 1 | 1 |
| 非高收入族 | 高收入族 | 总计 | |
| 赞成 | |||
| 不赞成 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
为了解某市市民对政府出台楼市限购令的态度,在该市随机抽取了50名市民进行调查,他们月收入(单位:百元)的频数分布及对楼市限购令的赞成人数如下表:
月收入 |
| [25,35) | [35,45) |
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 8 | 5 | 2 | 1 |
将月收入不低于55的人群称为“高收入族”,月收入低于55的人群称为“非高收人族”。
(Ⅰ)根据已知条件完成下面的2×2列联表,有多大的把握认为赞不赞成楼市限购令与收入高低有关?
已知: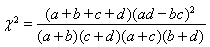 ,
,
当 <2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
<2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
当 >2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;
>2.706时,有90%的把握判定赞不赞成楼市限购令与收入高低有关;
当 >3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;
>3.841时,有95%的把握判定赞不赞成楼市限购令与收入高低有关;
当 >6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。
>6.635时,有99%的把握判定赞不赞成楼市限购令与收入高低有关。
| 非高收入族 | 高收入族 | 总计 |
赞成 |
|
|
|
不赞成 |
|
|
|
总计 |
|
|
|
(Ⅱ)现从月收入在[55,65)的人群中随机抽取两人,求所抽取的两人中至少一人赞成楼市限购令的概率。
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 9 | 12 | 5 | 1 | 1 |
| 非高收入族 | 高收入族 | 总计 | |
| 赞成 | |||
| 不赞成 | |||
| 总计 |
 ,n=a+b+c+d
,n=a+b+c+d| P(K2≥k) | 0.025 | 0.010 | 0.005 |
| k | 5.024 | 6.635 | 7.879 |
| 9R |
| 2 |
| OA1 |
| AA1 |
| OB1 |
| BB1 |
| OC1 |
| CC1 |
| S△OBC |
| S△ABC |
| S△OAC |
| S△ABC |
| S△OAB |
| S△ABC |
| AA1-R |
| AA1 |
| BB1-R |
| BB1 |
| CC1-R |
| CC1 |
| 1 |
| AA1 |
| 1 |
| BB1 |
| 1 |
| CC1 |
| 2 |
| R |
| 1 |
| AA1 |
| 1 |
| BB1 |
| 1 |
| CC1 |
| 9R |
| 2 |
| 16R |
| 3 |
| 16R |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com