2,4,6
二、选择题:
13.C 14.D 15.D 16.B
三、解答题:
17.解:设.files/image122.gif) 的定义域为D,值域为A
的定义域为D,值域为A
由.files/image124.gif) …………2分
…………2分
.files/image126.gif) …………4分
…………4分
又.files/image128.gif) …………6分
…………6分
.files/image130.gif) …………8分
…………8分
.files/image132.gif) 的定义域D不是值域A的子集
的定义域D不是值域A的子集
.files/image134.gif) 不属于集合M …………12分
不属于集合M …………12分
18.解:如图建立空间直角坐标系.files/image136.gif)
∵由题意可知∠C1AC=60°,C1C=.files/image138.gif) …………2分
…………2分
.files/image140.gif) 、
、.files/image142.gif) 、
、.files/image144.gif) 、
、.files/image146.gif) …………4分
…………4分
即.files/image148.gif) …………6分
…………6分
设.files/image150.gif)
则.files/image152.gif) …………8分
…………8分
.files/image154.gif) …………10分
…………10分
.files/image156.gif) …………12分
…………12分
19.解:(1).files/image158.gif) …………2分
…………2分
.files/image160.gif) …………4分
…………4分
.files/image162.gif)
.files/image164.gif) …………6分
…………6分
(2)设.files/image166.gif) …………8分
…………8分
则.files/image168.gif) …………10分
…………10分
.files/image170.gif) (m2) …………12分
(m2) …………12分
答:当.files/image172.gif) (m2) …………14分
(m2) …………14分
20.解:(1).files/image174.gif) =3
=3
.files/image176.gif) …………2分
…………2分
设圆心到直线l的距离为d,则
.files/image178.gif)
.files/image180.gif) 即直线l与圆C相离 …………6分
即直线l与圆C相离 …………6分
(2)由.files/image182.gif) …………8分
…………8分
由条件可知,.files/image184.gif) …………10分
…………10分
又∵向量的夹角的取值范围是[0,π]
.files/image186.gif) …………12分
…………12分
.files/image188.gif) …………14分
…………14分
21.解:(1).files/image190.gif)
.files/image192.gif)
.files/image194.gif) …………4分
…………4分
(2).files/image196.gif) …………5分
…………5分
.files/image198.gif)
.files/image200.gif) …………8分
…………8分
.files/image202.gif) …………10分
…………10分
(3).files/image204.gif)
.files/image206.gif) …………12分
…………12分
.files/image208.gif)
故103不是数列.files/image210.gif) 中的项 …………16分
中的项 …………16分
22.解:(1)易知.files/image212.gif) …………2分
…………2分
.files/image214.gif)
.files/image216.gif) …………4分
…………4分
(2).files/image218.gif)
.files/image220.gif)
.files/image222.gif) (*) …………6分
(*) …………6分
.files/image224.gif)
同理.files/image226.gif) …………8分
…………8分
.files/image228.gif)
.files/image230.gif) …………10分
…………10分
(3).files/image232.gif)
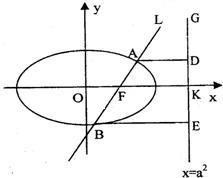
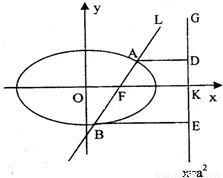
先探索,当m=0时,直线L⊥ox轴,则ABED为矩形,由对称性知,AE与BD相交于FK中点N
且.files/image234.gif) …………11分
…………11分
猜想:当m变化时,AE与BD相交于定点.files/image234.gif) …………12分
…………12分
证明:设.files/image237.gif)
当m变化时首先AE过定点N
.files/image239.gif)
∴KAN=KEN ∴A、N、E三点共线
同理可得B、N、D三点共线
∴AE与BD相交于定点.files/image234.gif) …………18分
…………18分

 如图,已知直线L:
如图,已知直线L: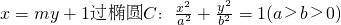 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.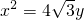 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;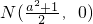 为x轴上一点,求证:
为x轴上一点,求证: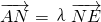 .
. 如图,已知直线L:
如图,已知直线L: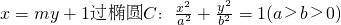 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.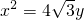 的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;
的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;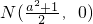 为x轴上一点,求证:
为x轴上一点,求证: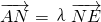 .
.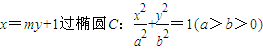 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E. 的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;
的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;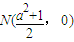 为x轴上一点,求证:
为x轴上一点,求证: .
.
 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E. 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程; 为x轴上一点,求证:
为x轴上一点,求证: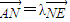 .
.
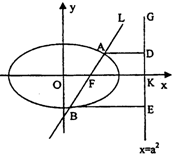 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C:.files/image112.gif) 5.5 6.―2 7.
5.5 6.―2 7..files/image114.gif) 8.
8..files/image116.gif) 9.18
9.18