
题目列表(包括答案和解析)
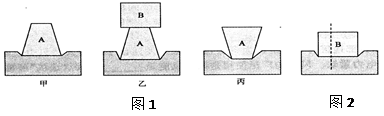
如果把连接梯形两腰的中点的线段叫做梯形的中位线,那么梯形的中位线有什么特征呢?
如图,在梯形ABCD中,AD∥BC,点E、F分别为两腰AB、CD的中点.则EF为梯形ABCD的中位线.仿照三角形的中位线定理,请你猜想EF的长与上、下底的关系.
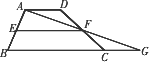
猜想:EF=________.
我们按如下思路探究:
(1)连接AF并延长交BC的延长线于点G,你发现△ADF和△GCF有怎样的关系?证明你的结论.
(2)由(1)的结论,可以得出EF是△ABG中怎样的线段?
(3)由此你能证明你的猜想吗?试一试.
 ,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2. 坐标又是什么?
坐标又是什么? ,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.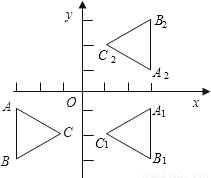
 ,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,-2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.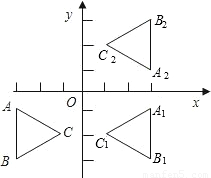
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com