
题目列表(包括答案和解析)
设有两个命题,p:关于x的不等式 (a>0,且a≠1)的解集是{x|x<0};q:函数
(a>0,且a≠1)的解集是{x|x<0};q:函数 的定义域为R。如果
的定义域为R。如果 为真命题,
为真命题, 为假命题,求实数a的取值范围。
为假命题,求实数a的取值范围。
设有两个命题,p:关于x的不等式 (a>0,且a≠1)的解集是{x|x<0};q:函数
(a>0,且a≠1)的解集是{x|x<0};q:函数 的定义域为R。如果
的定义域为R。如果 为真命题,
为真命题, 为假命题,则实数a的取值范围___________。
为假命题,则实数a的取值范围___________。
 (a>0,且a≠1)的解集是{x|x<0};q:函数
(a>0,且a≠1)的解集是{x|x<0};q:函数 的定义域为R。如果
的定义域为R。如果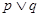 为真命题,
为真命题,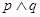 为假命题,则实数a的取值范围___________。
为假命题,则实数a的取值范围___________。 设有两个命题,p:关于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0};q:函数![]() 的定义域为R.如果
的定义域为R.如果![]() 为真命题,
为真命题,![]() 为假命题,则实数a的取值范围是________.
为假命题,则实数a的取值范围是________.
设有两个命题,p:关于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0};q:函数y=lg(ax2-x+a)的定义域为R.如果p![]() q为真命题,p
q为真命题,p![]() q为假命题,则实数a的取值范围是________.
q为假命题,则实数a的取值范围是________.
CBACA;DCADC;DB
30;9,27;1; 
17. 解:易得 ………… 3分
………… 3分
当a=1时, B= ,满足
,满足 ;
………… 5分
;
………… 5分
当 时,B={x|
时,B={x| 即B
即B A,
A,
必须 ,解之得
,解之得 ………… 8分
………… 8分
综上可知,存在这样的实数a 满足题设
满足题设 成立. ………… 10分
成立. ………… 10分
18. 解: (1) 图2是由四块图1所示地砖绕点 按顺时针旋转
按顺时针旋转 后得到,△
后得到,△ 为等腰直角三角形,
为等腰直角三角形,
 四边形
四边形 是正方形.
……
4分
是正方形.
……
4分
(2) 设 ,则
,则 ,每块地砖的费用为
,每块地砖的费用为 ,制成△
,制成△ 、△
、△ 和四边形
和四边形 三种材料的每平方米价格依次为
三种材料的每平方米价格依次为


 . …… 10分
. …… 10分
由 ,当
,当 时,
时, 有最小值,即总费用为最省.
有最小值,即总费用为最省.
答:当 米时,总费用最省. …… 12分
米时,总费用最省. …… 12分
19. 解:(Ⅰ)易得 ,
, 的解集为
的解集为 ,
, 恒成立.
恒成立. 解得
解得 .………………… 3分
.………………… 3分
因此 的对称轴
的对称轴 , 故函数
, 故函数 在区间
在区间 上不单调,从而不存在反函数。
……………………… 5分
上不单调,从而不存在反函数。
……………………… 5分
(Ⅱ)由已知可得 ,则
,则
 ,
,
令 得
得 .
………………………7分
.
………………………7分
①
若 ,则
,则 在
在 上单调递增,在
上单调递增,在 上无极值;
上无极值;
②
若 ,则当
,则当 时,
时, ;当
;当 时,
时, .
.
 当
当 时,
时, 有极小值
有极小值 在区间
在区间 上存在极小值,
上存在极小值, .
.
③
若 ,则当
,则当 时,
时, ;当
;当 时,
时, .
.
 当
当 时,
时, 有极小值.
有极小值.

 在区间
在区间 上存在极小值
上存在极小值  .……………… 10分
.……………… 10分
综上所述:当 时,
时, 在区间
在区间 上存在极小值。………… 12分
上存在极小值。………… 12分
20. 解:(Ⅰ)当 时,
时,
故 ,即数列的通项公式为
,即数列的通项公式为 …… 4分
…… 4分
(Ⅱ)当 时,
时,
当
 …… 8分
…… 8分

由此可知,数列 的前n项和
的前n项和 为
为 …… 12分
…… 12分
21. 解:(Ⅰ) .
…… 4分
.
…… 4分
(Ⅱ)易得 的值域为A=
的值域为A= ,设函数
,设函数 的值域B,若对于任意
的值域B,若对于任意 总存在
总存在 ,使得
,使得 成立,只需
成立,只需 。
…… 6分
。
…… 6分
显然当 时,
时, ,不合题意;
,不合题意;
当 时,
时, ,故应有
,故应有 ,解之得:
,解之得: ;…… 8分
;…… 8分
当 时,
时, ,故应有
,故应有 ,解之得:
,解之得: 。…… 10分
。…… 10分
综上所述,实数 的取值范围为
的取值范围为 。
…… 12分
。
…… 12分
22. 解:(Ⅰ) .
.
…… 3分
(Ⅱ)  …… 6分
…… 6分
 ,
,
由错位相减法得: ,
,


所以: 。 …… 8分
。 …… 8分
(Ⅲ) 
 为递增数列 。
为递增数列 。
 中最小项为
中最小项为 …… 12分
…… 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com