
题目列表(包括答案和解析)
已知函数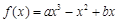 (
(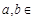 R),
R),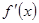 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值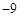 .
.
(1)求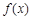 的单调递减区间;
的单调递减区间;
(2)若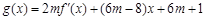 ,
,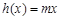 ,当
,当 时,对于任意x,
时,对于任意x,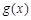 和
和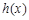 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围;
(3)若不等式 (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求 的最大值.
的最大值.
已知函数 (
( R),
R), 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值 .
.
(1)求 的单调递减区间;
的单调递减区间;
(2)若 ,
, ,当
,当 时,对于任意x,
时,对于任意x, 和
和 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围;
(3)若不等式 (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求 的最大值.
的最大值.
 (
( R),
R),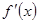 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值 .
.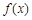 的单调递减区间;
的单调递减区间; ,
, ,当
,当 时,对于任意x,
时,对于任意x, 和
和 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围; (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求 的最大值.
的最大值.已知函数![]()
(I)若![]() 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数![]() 的最小值;
的最小值;
(III)设函数![]() 的图象C1与函数
的图象C1与函数![]() 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
已知函数![]()
(1)若![]() 时,函数
时,函数 ![]() 在其定义域内是增函数,求b的取值范围
在其定义域内是增函数,求b的取值范围
(2)在(1)的结论下,设函数![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设函数![]() 的图象C1 与函数
的图象C1 与函数![]() 的图象C2 交于P,Q两点,过线段PQ的中点R作x轴的垂线分别交C1、C2于M、N两点,问是否存在点R,使C1 在M处的切线与C2 在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。
的图象C2 交于P,Q两点,过线段PQ的中点R作x轴的垂线分别交C1、C2于M、N两点,问是否存在点R,使C1 在M处的切线与C2 在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。
一、 1.A 2.C 3.C 4.B 5.A 6.C
7.D 8.C 9.B 10.D 11.A 12.C
二、13..files/image189.gif) 14.0 15.
14.0 15..files/image191.gif) 16.①②④ .
16.①②④ .
三、
17.解:解:.files/image193.gif) ---------------------------------3分
---------------------------------3分
.files/image195.gif) ---------------------------------------------------6分
---------------------------------------------------6分
因为.files/image197.gif) , ---------------------------------------------------------------8分
, ---------------------------------------------------------------8分
所以.files/image199.gif) ---------------------------------------------------------------------10分
---------------------------------------------------------------------10分
解得.files/image201.gif) ,故实数
,故实数.files/image024.gif) 的取值范围为[0,1] --------------------------------------12分
的取值范围为[0,1] --------------------------------------12分
18.解:由条件知.files/image203.gif) ,
,.files/image205.gif) ----------------4分
----------------4分
①当.files/image207.gif) 时,
时,
.files/image209.gif)
.files/image211.gif)
.files/image213.gif)
.files/image215.gif) ---------------------------------------------------------------------------------------7分
---------------------------------------------------------------------------------------7分
②当.files/image217.gif)
.files/image219.gif)
.files/image221.gif)
.files/image223.gif) ----------------------------------------------------------------------------------------------10分
----------------------------------------------------------------------------------------------10分
纵上所述,.files/image225.gif) 的值域为
的值域为.files/image227.gif) -----------------------------------------------------------------------12分19.(I)解:因为α为第二象限的角,
-----------------------------------------------------------------------12分19.(I)解:因为α为第二象限的角,.files/image229.gif) ,
,
所以,.files/image231.gif) ,------------------------------------------------2分
,------------------------------------------------2分
.files/image233.gif) ------------------------------------------------------------------ 4分
------------------------------------------------------------------ 4分
又.files/image235.gif) ,
,
所以,.files/image237.gif) ---------------------------------------- 6分
---------------------------------------- 6分
(II)解:因为β为第三象限的角,.files/image235.gif) ,
,
所以,.files/image240.gif) ------------------------------------------------------------8分
------------------------------------------------------------8分
又.files/image242.gif) ,--------------------10分
,--------------------10分
所以,.files/image244.gif) -----------------------------12分
-----------------------------12分
20.解:(I)由.files/image175.gif) ,得
,得.files/image247.gif) ,
,
所以.files/image249.gif)
整理,得.files/image251.gif) --------------------------------------------------------4分
--------------------------------------------------------4分
解得:.files/image253.gif) ,∴
,∴ .files/image255.gif) --------------------------------------------------------6分
--------------------------------------------------------6分
(II)由余弦定理得:.files/image257.gif) ,即
,即.files/image259.gif) ---------①
---------①
又.files/image261.gif) ,∴
,∴.files/image263.gif) ------------------------------------------------②,
------------------------------------------------②,
①②联立解得,.files/image265.gif) -------------------------------------------------------------------- 10分
-------------------------------------------------------------------- 10分
∴.files/image267.gif) --------------------------------------------------12分
--------------------------------------------------12分
21.解:(Ⅰ)∵f(x)图象过点(1,8),∴a−5+c+d=8,
即a+c+d=13 ① …………………………1分
又f/(x)=3ax2−10x+c,且点(1,8)处的切线经过(3,0),
∴f/(1)=.files/image269.gif) = −4,即
= −4,即
∴
又∵f(x)在x=3 处有极值,∴f/(3)=0,
即
联立①、②、③解得a=1,c=3,d=9,
∴f(x)=x3−5x2+3x+9 …………………………6分
(Ⅱ)f/(x)=3x2−10x+3=(3x−1)(x−3)
由f/(x)=0得x1=.files/image271.gif) ,x2=3
………………………7分
,x2=3
………………………7分
当x∈(0,.files/image271.gif) )时,f/(x)>0,f(x)单调递增,
)时,f/(x)>0,f(x)单调递增,
∴f(x)>f(0)=9 ………………………9分
当x∈(.files/image271.gif) ,3)时,f/(x)<0,f(x)单调递减,
,3)时,f/(x)<0,f(x)单调递减,
∴f(x)>f(3)=0.
又∵f(3)=0,
∴当m>3时,f(x)>0在(0,m)内不恒成立. ………………………11分
∴当且仅当m∈(0,3]时,f(x)>0在(0,m)内恒成立.
所以m取值范围为(0,3] . ………………………12分
22.(I)解:对函数.files/image274.gif) ------------------------------------- 2分
------------------------------------- 2分
要使.files/image276.gif) 上是增函数,只要
上是增函数,只要.files/image278.gif) 上恒成立,
上恒成立,
即.files/image280.gif) 上恒成立------------------------------------------------4分
上恒成立------------------------------------------------4分
因为.files/image282.gif) 上单调递减,所以
上单调递减,所以.files/image282.gif) 上的最小值是
上的最小值是.files/image285.gif) ,
,
注意到a > 0,所以a的取值范围是.files/image287.gif) ----------------------------------------------6分
----------------------------------------------6分
(II)解:①当.files/image289.gif) 时,由(I)知,
时,由(I)知,.files/image291.gif) 上是增函数,
上是增函数,
此时.files/image291.gif) 上的最大值是
上的最大值是.files/image293.gif) ---------------------------8分
---------------------------8分
②当.files/image295.gif) ,
,
解得.files/image297.gif) ---------------------------------------------------------------------10分
---------------------------------------------------------------------10分
因为.files/image299.gif) ,
,
所以.files/image301.gif) 上单调递减,
上单调递减,
此时.files/image291.gif) 上的最大值是
上的最大值是.files/image303.gif) ----------------------13分
----------------------13分
综上,当.files/image289.gif) 时,
时,.files/image291.gif) 上的最大值是
上的最大值是.files/image306.gif) ;
;
当.files/image308.gif) 时,
时,.files/image291.gif) 上的最大值是
上的最大值是.files/image310.gif) --------------------------14分
--------------------------14分
| ||||||||||||||