
题目列表(包括答案和解析)
设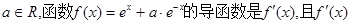 是奇函数,若曲线
是奇函数,若曲线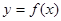 的一条切线的斜率是
的一条切线的斜率是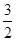 ,则切点的横坐标为 ( )
,则切点的横坐标为 ( )
A.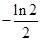 B.—
B.—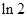 C.
C.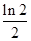 D.
D.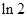
(本题满分18分,第1小题6分,第2小题6分,第3小题6分)
对于定义在D上的函数 ,若同时满足
,若同时满足
(Ⅰ)存在闭区间 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数);
(Ⅱ)对于D内任意 ,当
,当 时总有
时总有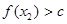 ,则称
,则称 为“平底型”函数。
为“平底型”函数。
(1)判断 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若 ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。
设 ,函数
,函数 的导函数
的导函数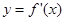 是奇函数,若曲线
是奇函数,若曲线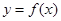 的一条切线斜率为
的一条切线斜率为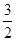 ,则切点的横坐标为 ( )
,则切点的横坐标为 ( )
A.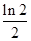 B.
B.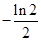 C.
C.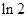 D.
D.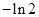
设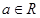 ,函数
,函数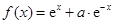 的导函数是
的导函数是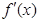 ,且
,且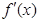 是奇函数,若曲线
是奇函数,若曲线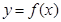 的一条切线的斜率是
的一条切线的斜率是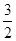 ,则切点的横坐标为( )
,则切点的横坐标为( )
A. 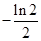 B.
B.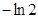 C.
C.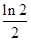 D.
D. 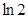
已知函数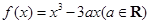 ,若直线
,若直线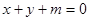 对任意的
对任意的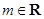 都不是曲线
都不是曲线 的切线,则
的切线,则 的取值范围是 .
的取值范围是 .
一、选择题
1.C 2.B 3.C 4.C 5.A 6.C
7.B 8.D 9.C 10.C 11.D 12.D
二、填空题
13..files/image190.gif) 14.3 15.
14.3 15..files/image192.gif) 16.②
16.②
三、解答题
17.解:由.files/image194.gif) 得
得.files/image196.gif) ,
---------------2分
,
---------------2分
则.files/image198.gif) =3,即
=3,即.files/image200.gif) ,
---------------8分
,
---------------8分
从而.files/image137.gif)
.files/image203.gif) ----------------12分
----------------12分
18. 解:(1)∵f (x)=2sinxcos.files/image205.gif) +cos x+a=
+cos x+a=.files/image207.gif) sin x+cos x+a
sin x+cos x+a
=2sin(x+.files/image205.gif) )+a, ……4分
)+a, ……4分
∴函数f(x)的最小正周期T=2π. ……6分
(Ⅱ)∵x∈[-.files/image210.gif) ,
,.files/image210.gif) ],∴-
],∴-.files/image213.gif) ≤x+
≤x+.files/image205.gif) ≤
≤.files/image216.gif) .
…….7分
.
…….7分
∴当x+.files/image205.gif) =-
=-.files/image213.gif) ,即x=-
,即x=-.files/image210.gif) 时, fmin(x)=f(-
时, fmin(x)=f(-.files/image210.gif) )=-
)=-.files/image146.gif) +a; ……9分
+a; ……9分
当x+.files/image205.gif) =
=.files/image210.gif) ,即x=
,即x=.files/image213.gif) 时, fmax(x)=f(
时, fmax(x)=f(.files/image213.gif) )=2+a.
……11分
)=2+a.
……11分
由题意,有(-.files/image146.gif) +a)+(2+a)=
+a)+(2+a)=.files/image146.gif) .
.
∴a=.files/image146.gif) -1.
……12分
-1.
……12分
19.(本小题满分12分)
(1)由题意得.files/image058.gif) 的最小正周期为
的最小正周期为.files/image231.gif) -----------2分
-----------2分
.files/image233.gif) -------------4分
-------------4分
.files/image235.gif)
又.files/image152.gif) 是它的一个对称中心,
是它的一个对称中心,
.files/image237.gif) ----------------------6分
----------------------6分
.files/image239.gif) ------------------------7分
------------------------7分
(2)因为.files/image241.gif) ,
------------------------8分
,
------------------------8分
.files/image243.gif)
所以欲满足条件,必须.files/image245.gif) -------------------11分
-------------------11分
.files/image247.gif)
即a的最大值为.files/image249.gif) -------------------12分
-------------------12分
20. 解:(Ⅰ)当每辆车的月租金定为3600元时,未租出的车辆数为.files/image251.gif) ,
,
所以这时租出了88辆车. -----------------------4分
(Ⅱ)设每辆车的月租金定为x元,则租赁公司的月收益为
.files/image253.gif) ,
-------------------------8分
,
-------------------------8分
整理得.files/image255.gif) .
.
所以,当x=4100时,.files/image058.gif) 最大,最大值为
最大,最大值为.files/image258.gif) ,
,
即当每辆车的月租金定为4100元时,租赁公司的月收益最大,
最大月收益为304200元. --------------------12分
21.解: (Ⅰ)∵.files/image058.gif) 为奇函数,∴
为奇函数,∴.files/image261.gif)
即.files/image263.gif)
∴.files/image265.gif) ----------------------1分
----------------------1分
∵.files/image267.gif) 的最小值为
的最小值为.files/image171.gif) ,
,
.files/image269.gif) -----------3分
-----------3分
又直线.files/image169.gif) 的斜率为
的斜率为.files/image271.gif)
因此,.files/image273.gif) ------------5分
------------5分
∴.files/image275.gif) ,
,.files/image277.gif) ,
,.files/image265.gif) .
-------------6分
.
-------------6分
(Ⅱ).files/image280.gif) .
.
.files/image282.gif) ,列表如下:
,列表如下:
.files/image284.gif)
.files/image286.gif)
.files/image288.gif)
.files/image290.gif)
.files/image292.gif)
.files/image294.gif)
.files/image091.gif)
.files/image297.gif)
.files/image299.gif)
.files/image301.gif)
.files/image299.gif)
.files/image297.gif)
得分 评卷人
.files/image058.gif)
.files/image305.gif)
极大
.files/image307.gif)
极小
.files/image305.gif)
所以函数.files/image058.gif) 的单调增区间是
的单调增区间是.files/image286.gif) 和
和.files/image294.gif) . -----------9分
. -----------9分
∵.files/image312.gif) ,
,.files/image314.gif) ,
,.files/image316.gif)
∴.files/image058.gif) 在
在.files/image178.gif) 上的最大值是
上的最大值是.files/image316.gif) ,最小值是
,最小值是.files/image314.gif) . ---------12分
. ---------12分
22. 解:(1).files/image318.gif) 是奇函数,
是奇函数,
.files/image322.gif)
.files/image324.gif) ------------------4分
------------------4分
(2)又.files/image326.gif) 在[-1,1]上单调递减,
在[-1,1]上单调递减,.files/image328.gif) ------6分
------6分
.files/image330.gif) ----------------------------------------------------8分
----------------------------------------------------8分
.files/image332.gif)
令.files/image334.gif)
则.files/image336.gif) ----------------------------12分
----------------------------12分
.files/image338.gif)
.files/image340.gif)
.files/image184.gif) -------------------------------14分
-------------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com