
题目列表(包括答案和解析)
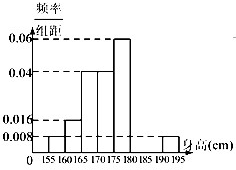 从某校高三年级800名男生中随机抽取50名学生测量其身高,据测量被测学生的身高全部在155cm到195cm之间.将测量结果按如下方式分成8组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组得到的频率分布直方图的一部分.已知:第1组与第8组的人数相同,第6组、第7组和第8组的人数依次成等差数列.?
从某校高三年级800名男生中随机抽取50名学生测量其身高,据测量被测学生的身高全部在155cm到195cm之间.将测量结果按如下方式分成8组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组得到的频率分布直方图的一部分.已知:第1组与第8组的人数相同,第6组、第7组和第8组的人数依次成等差数列.?| 分组 | 频数 | 频率 | 频率/组距 |
| … | … | … | … |
| [180,185) | x | y | z |
| [185,190) | m | n | p |
| … | … | … | … |
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
|
|
男性 |
女性 |
合计 |
|
反感 |
10 |
|
|
|
不反感 |
|
8 |
|
|
合计 |
|
|
30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是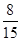 .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
|
P(K2>k) |
0.05 |
0.025 |
0.010 |
0.005 |
|
k |
3.841 |
5.024 |
6.635 |
7.879 |
下面的临界值表供参考:
(参考公式:K2=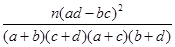 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)"
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
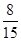 .
.| P(K2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.841 | 5.024 | 6.635 | 7.879 |
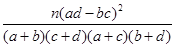 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)" 已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
| 分 组 | 频 数 | 频 率 |
| [80,90) | x | 0.04 |
| [90,100) | 9 | y |
| [100,110) | z | 0.38 |
| [110,120) | 17 | 0.34 |
| [120,130] | 3 | 0.06 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com