
题目列表(包括答案和解析)
 [选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分.
[选做题]在下面A,B,C,D四个小题中只能选做两题,每小题10分,共20分.
|
| π |
| 4 |
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤。
A.选修4—1:几何证明选讲
如图,△ABC是![]() 的内接三角形,PA是
的内接三角形,PA是![]() 的切线,PB交AC于点E,交
的切线,PB交AC于点E,交![]() 于点D.若
于点D.若
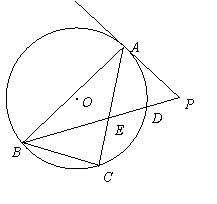 PE=PA,
PE=PA,![]() ,PD=1,BD=8,求BC的长.
,PD=1,BD=8,求BC的长.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤。
A.选修4—1:几何证明选讲
如图,△ABC是![]() 的内接三角形,PA是
的内接三角形,PA是![]() 的切线,PB交AC于点E,交
的切线,PB交AC于点E,交![]() 于点D.若
于点D.若
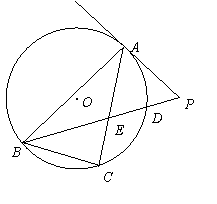 PE=PA,
PE=PA,![]() ,PD=1,BD=8,求BC的长.
,PD=1,BD=8,求BC的长.
[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内
(选修4—1:几何证明选讲)
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,![]() ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
【选做题】在A、B、C、D四小题中只能选做两题.每小题l0分.共计20分.请在答题纸指定 区域内作答.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
如图,在△ABC中,D是AC中点,E是BD三等分点,AE的延长线交口BC于F,求![]() 的值.
的值.

B.选修4-2:矩阵与变换
已知矩阵M=![]()
![]() ,求矩阵M的特征值及其相应的特征向量.
,求矩阵M的特征值及其相应的特征向量.

选择题:
1―5 ACCAC 6―10 DCBBB 11―12 BC
填空题:
13.[1,2]递增,递增 14.2 15.3 16.
解答题:
17.解:①
②若
18.解:①
②公比为2的等比数列。
19.解:建立如图所示的空间坐标系,
(1)
…………2分
(2)设面ABCD的法向量为即
………………6分
∴EG和平面ABCD所成的角为30° ………………8分
(3)设平面DFC的法向量为
………………10分
∴二面角B―DC―F的余弦值为0 ………………12分
20.(1)设椭圆C的方程为
…………4分
(2)证明:设
①PA,PB都不与x轴垂直,且
②PA或PB与x轴垂直或 ………………12分
21.解:(1)
(2)令
(3)用数学归纳法证。
①当
由(2)得
②当
22.解:由于△BCD是正三角形,且B、D、C、Q四点共圆,所以∠BQD=∠BCD=60°
则∠AQB=180°―∠BAD=120°,同理得∠CQA=120°
又Q点Q在△ABC的内部,∴点Q就是△ABC的费马点。
解:以A为极点,AB所在直线为极轴,建立极坐标系。
w.w.w.k.s.5.u.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com