（本小题满分15分）
已知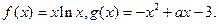
（Ⅰ）求函数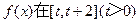上的最小值；
（Ⅱ）若对一切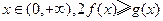恒成立，求实数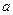的取值范围；
（Ⅲ）证明：对一切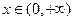，都有成立.

（本小题满分15分）已知函数，,．

??????（Ⅰ） 求函数的极大值点与极小值点；??（Ⅱ） 若函数在上有零点，求的最大值（ 为自然对数的底数）；??????（Ⅲ） 设（），试问数列中是否存在相等的两项？若存在，求出所有相等的两项；若不存在，请说明理由．

（本小题满分15分）

某旅游商品生产企业，2009年某商品生产的投入成本为1元/件，

出厂价为流程图的输出结果元/件，年销售量为10000件，

因2010年国家长假的调整，此企业为适应市场需求，

计划提高产品档次，适度增加投入成本．若每件投入成本增加的

比例为（），则出厂价相应提高的比例为，

同时预计销售量增加的比例为．

已知得利润（出厂价投入成本）年销售量．

（Ⅰ）写出2010年预计的年利润

与投入成本增加的比例的关系式；

（Ⅱ）为使2010年的年利润比2009年有所增加，

问：投入成本增加的比例应在什么范围内？

（本小题满分15分）设是公比大于1的等比数列，为数列的前项和．已知，且构成等差数列．

（1）求数列的通项公式.（2）令求数列的前项和．

（本小题满分15分）已知函数.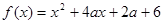

(1)若函数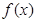的值域为，求a的值；

(2)若函数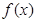在上是增函数,求实数的取值范围．