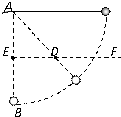如图所示，质量为m的小球，由长为l的细线系住，线能承受的最大拉力是9mg，细线的另一端固定在A点，AB是过A的竖直线，E为AB上的一点，且AE=0.5l，过E作水平线EF，在EF上钉铁钉D，现将小球拉直水平，然后由静止释放，小球在运动过程中，不计细线与钉子碰撞时的能量损失，不考虑小球与细线间的碰撞．
（1）若钉铁钉位置在E点，求细线与钉子碰撞前后瞬间，细线的拉力分别是多少？
（2）若小球能绕钉子在竖直面内做完整的圆周运动，求钉子位置在水平线EF上距E点距离的取值．

查看答案和解析>>

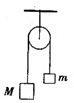如图所示，质量分别为M和m的物体用细线连接，悬挂在定滑轮上，定滑轮固定在天花板上，已知M＞m，且线与滑轮的摩擦和滑轮及线的质量都忽略不计．在两物体运动的过程中（未触及定滑轮之前），下列说法中正确的是（　　）

A．在任意时刻，M的速度都大于m的速度

B．在任意时刻，M的加速度都大于m的加速度

C．细线的拉力一定大于mg

D．细线的拉力等于 2Mmg M+m

查看答案和解析>>

如图所示，质量为m的滑块在水平面上撞向弹簧，当滑块将弹簧压缩了x₀时速度减小到零，然后弹簧又将滑块向右推开．已知弹簧的劲度系数为k，滑块与水平面间的动摩擦因数为μ，整个过程弹簧未超过弹性限度，则（　　）

A．滑块向左接触弹簧的运动过程中，始终做减速运动

B．滑块向右接触弹簧的运动过程中，始终做加速运动

C．滑块与弹簧接触过程中最大加速度为 kx0+μmg m

D．滑块向右运动过程中，当弹簧形变量x= μmg k 时，物体的动能最大

查看答案和解析>>

如图所示，质量为m₁的物体甲通过三段轻绳悬挂，三段轻绳的结点为O．轻绳OB水平且B端与放置在水平面上的质量为m₂的物体乙相连，轻绳OA与竖直方向的夹角θ=37°，物体甲、乙均处于静止状态．（已知：sin37°=0.6，cos37°=0.8）求：
（1）轻绳OA、OB受到的拉力是多大？
（2）物体乙受到的摩擦力是多大？方向如何？

查看答案和解析>>

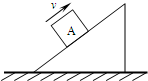如图所示，质量为m的物体A以一定的初速度v沿粗糙斜面上滑，物体A在上滑过程受到的力有（　　）

A．向上有冲力、重力、斜面上的支持力，沿斜面向下的摩擦力

B．重力、斜面的支持力

C．重力、对斜面上的正压力、沿斜面向下的摩擦力

D．重力、斜面的支持力、沿斜面向下的摩擦力

查看答案和解析>>

物理

1、C  2、BCD  3、A  4、AC  5、D  6、B   7、BD  8、D  9、ACD   10、D

11.  (1)2.600    2.030    　

12. （全对才得分）(1)BCF   (2)BD  (3) 65.7(65.2---66.0都给分)   ABD

13.:设转速为n

对上图有:水平方向 Nsinθ-fcosθ=m4π²nr……………①   2^/

       竖直方向上有Ncosθ+fsinθ=mg   ……………②   2^/

                F=μN        …………………………③   1^/

联立方程有    

对下图有:水平方向 Nsinθ+fcosθ=m4π²nr  ……………①   1^/

       竖直方向上有Ncosθ-fsinθ=mg     ……………②   1^/

                F=μN          …………………………③   

联立方程有  

综上可知：  3^/

14解：（1）在轨道I上，飞行器所受万有引力提供向心力，设地球质量为M，则有

　　      ………………………2^/

同理在轨道II上        ………………………1^/ 

由上式可得                   ………………………1^/

　　在轨道I上重力加速度为g′，则有………………………2^/

　　可得    ………………………1^/

（2）设喷出气体质量为△m，由动量守恒得：……2^/              ……………………… ………………………1^/

　　17. (1)由图线读得，转盘的转动周期T＝0.8s  ………………………①   1分

角速度         ………………………②    2分

(2)激光器和探测器沿半径由中心向边缘移动(理由为：由于脉冲宽度在逐渐变窄，表明光信号能通过狭缝的时间逐渐减少，即圆盘上对应探测器所在位置的线速度逐渐增加，因此激光器和探测器沿半径由中心向边缘移动)．                              2分

(3)设狭缝宽度为d，探测器接收到第i个脉冲时距转轴的距离为r₁，第i个脉冲的宽度为△t_i，激光器和探测器沿半径的运动速度为v．

                                    　　　　 　　　③  1分

            r₃－r₂＝r₂－r₁＝vT                        　　　　 　④   1分

            r₂－r₁＝　　　　　　　　　　　　　　　⑤   1分

r₃－r₂＝                    　　　　　⑥   1分

由④、⑤、⑥式解得：

                7  2分

18、若m₁＞m₂时，碰撞后系统的总动量方向向左，

设它们相对静止时的共同速度为V^/，据动量守恒定律， 有：m₁V-m₂V=(m₁+m₂)V’

所以V^/=(m₁-m₂)V/(m₁+m₂)                     2分

若相对静止时B正好在A的右端，则系统机械能损失应为μm₂gL，

则据能量守恒：       2分

解得：V=                              1 分

若m₁=m₂时，碰撞后系统的总动量为零，最后都静止在水平面上，  1分

设静止时A在B的右端，则有：          2分

 解得：V=    带入        2分

若m₁＜m₂时，则A和墙壁能发生多次碰撞，每次碰撞后总动量方向都向右，

设最后A静止在靠近墙壁处时，B静止在A的右端，   1分

同理有：             1分

解得：V=           2 分

故：若m₁＞m₂，V必须小于或等于

若m₁＜m₂，V必须小于或等于      

若m₁＝m₂  V必须等于