
题目列表(包括答案和解析)
 既是奇函数,又是偶函数;
既是奇函数,又是偶函数;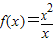 为同一函数;
为同一函数;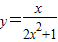 的值域为
的值域为 .
. 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为 .
. 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为 .
. 既是奇函数,又是偶函数;
既是奇函数,又是偶函数; 为同一函数;
为同一函数; 的值域为
的值域为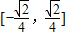 .
.已知函数f(x)的定义域为R,且满足f(-x)=![]() >0,又g(x)=f(x)+c(c为常数),在区间[a,b](a<b)上是单调递减函数,判断并证明g(x)在[-b,-a]上的单调性.
>0,又g(x)=f(x)+c(c为常数),在区间[a,b](a<b)上是单调递减函数,判断并证明g(x)在[-b,-a]上的单调性.
思路分析:根据函数增减性的定义,在[-b,-a]上任取两个值x1,x2,且x1<x2,进而判断g(x1)-g(x2)的正负.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com