1,3,5
13.-1 14. 15.
15. 16.②③
16.②③
三、解答题(本大题共6小题,共计70分)
17.(本小题满分10分)
解:化简条件得 …………2分
…………2分
根据集合中元素个数集合B分类讨论,
当
 …………4分
…………4分
当 …………6分
…………6分
当 …………2分
…………2分
 …………8分
…………8分
综上所述, …………10分
…………10分
18.(本小题满分12分)
解:
 …………2分
…………2分
即 …………4分
…………4分

即 …………8分
…………8分
又
 …………10分
…………10分

…………12分
19.(本小题满分12分)
解:(1)取出的两个球都是黑球,则甲盒恰好有两个黑球的事件记为A1,
 …………2分
…………2分
取出的两个球都是红球,则甲盒恰好有两个黑球的事件记为A2,
 …………4分
…………4分
所以 …………6分
…………6分
(2) …………7分
…………7分
 …………8分
…………8分
 …………9分
…………9分
ξ得分布列为

 …………12分
…………12分
20.(本小题满分12分)
证明:(I)在直三棱柱ABC-A1B1C1中,易知面ACC1A1⊥面ABC,
∵∠ACB
= 90°,
∴BC⊥面ACC1A1, …………2分
∵AM 面ACC1A1
面ACC1A1
∴BC⊥AM
∵AM⊥BA1,且BC∩BA1=B
∴AM⊥平面A1BC …………4分
(II)设AM与A1C的交点为O,连结BO,由(I)可知AM⊥OB,且AM⊥OC,所以∠BOC为二面角B
? AM ? C的平在角 …………5分
在Rt△ACM和Rt△A1AC中,∠OAC
+∠ACO=90°,
∴∠AA1C
=∠MAC
∴Rt△ACM∽Rt△A1AC
∴AC2 = MC?AA1
 …………7分
…………7分

 ,故所求二面角的大小为45° …………9分
,故所求二面角的大小为45° …………9分
(III)设点C到平面ABM的距离为h,易知BO= ,
,
可得 …………10分
…………10分

∴点C到平面ABM的距离为 …………12分
…………12分
解法二:(I)同解法一
(II)如图以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则

即 …………6分
…………6分
设向量 ,则
,则
 的平面AMB的一个法向量为
的平面AMB的一个法向量为
 是平面AMC的一个法向量 …………8分
是平面AMC的一个法向量 …………8分

易知, 所夹的角等于二面角B ? AM ? C的大小,故所求二面角的大小为45°
所夹的角等于二面角B ? AM ? C的大小,故所求二面角的大小为45°
…………9分
(III)向量 即为所求距离 …………10分
即为所求距离 …………10分
 …………12分
…………12分
∴点C到平面ABM的距离为 …………12分
…………12分
21.(本小题满分12分)
(1)解: ,
,
 ,
,
即 …………3分
…………3分
 ,
,
 …………6分
…………6分
(II)由(I)及 , …………8分
, …………8分
 ,
,
 (1)
(1)
 (2)
(2)
(2)-(1)得,
 …………10分
…………10分
要使
 成立的正整数n的最小值为5. …………12分
成立的正整数n的最小值为5. …………12分
22.(本小题满分12分)
解:(I) …………2分
…………2分
 处的切线互相平行
处的切线互相平行
 …………3分
…………3分

 …………4分
…………4分
(II)

 …………5分
…………5分

 …………7分
…………7分

 …………9分
…………9分
∴满足条件的a的值满足下列不等式组
 ①,或
①,或 ②
②
不等式组①的解集为空集,解不等式组②得
综上所述,满足条件的a的取值范围是: …………12分
…………12分

![]() 的图象经过三点
的图象经过三点![]() .
.![]()
![]() 的解析式(2)求函数
的解析式(2)求函数![]() 在区间
在区间![]() 上的最大值和最小值
上的最大值和最小值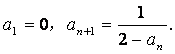
![]() ;
;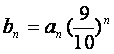 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有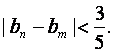
![]() ,其中a为常数.
,其中a为常数. ![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;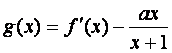 的单调区间.
的单调区间.![]() ,乙投篮命中的概率为
,乙投篮命中的概率为![]()
![]() 是椭圆
是椭圆![]() 的两个焦点,O为坐标原点,点
的两个焦点,O为坐标原点,点![]() 在椭圆上,且
在椭圆上,且![]() ,圆O是以
,圆O是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆O相切,并且与椭圆交于不同的两点A、B.
与圆O相切,并且与椭圆交于不同的两点A、B.![]()
![]()
![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.