查看答案和解析>>

已知分别是圆锥曲线和的离心率，设
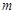，则的取值范围是

A．（，0）

B．（0，）

C．（，1）

D．（1，）

查看答案和解析>>

查看答案和解析>>

已知分别是圆锥曲线和的离心率，设，则的取值范围是              .

查看答案和解析>>

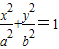已知a＞b＞0，e₁，e₂分别是圆锥曲线和的离心率，设m=lne₁+lne₂，则m的取值范围是     ．

查看答案和解析>>

一、

1．B       2．A      3．D      4．A      5．C      6．A      7．D      8．B       9．D      10．A

11．A    12．B

1．由题意知，解得．

2．由得，化得，解得．

3．，又．

4．设到的角为的斜率的斜率，

则，于是．

5．由条件，解即得，则．

6．不等式组化得 

       平面区域如图所示，阴影部分面积：

       ．

7．由已知得，而

       ，则是以3为公比的等比数列．

8．即，于是，而解得．

9．函数可化为，令，

       可得其对称中心为，当时得对称中心为．

10．．

11．由条件得：，则得所以．

12．沿球面距离运动路程最短，最短路程可以选

       ．

二、填空题

13．

       ，由与垂直得．即

       ，解得

14．99

       在等差数列中，也是等差数列，由等差中项定理得．

       所以．

15．

由题意知，直线是抛物线的准线，而到的距离等于到焦点的距离．即求点到点的距离与到点的距离和的最小值，就是点与点的距离，为．

16．②

一方面．由条件，，得，故②正确．

另一方面，如图，在正方体中，把、分别记作、，平面、平面、平面分别记作、、，就可以否定①与③．

三、解答题

17．解：，且

       ，即

       又．

       由余弦定理，

       ，故．

18．解：（1）只有甲解出的概率：．

       （2）只有1人解出的概率：．

19．解：（1）由已知，∴数列的公比，首项

              又数列中，

           ∴数列的公差，首项

           ∴数列、的通项公式依次为．

（2），

       ．

20．（1）证明；在直三棱柱中，

              面

              又

              面，而面，

           ∴平面平面

（2）解：取中点，连接交于点，则．

与平面所成角大小等于与平面所成角的大小．

取中点，连接、，则等腰三角形中，．

又由（1）得面．

面

为直线与面所成的角

又

，

∴直线与平面所成角的正切值为．

（注：本题也可以能过建立空间直角坐标系解答）

21．解：（1）设椭圆方程为，双曲线方程为

              ，半焦距

              由已知得，解得，则

              故椭圆及双曲线方程分别为及．

       （2）向量与的夹解即是，设，则

              由余弦定理得           ①

        由椭圆定义得                    ②

        由双曲线定义得                   ③

        式②+式③得，式②式③得

将它们代入式①得，解得，所以向量与夹角的余弦值为．

22．解（1）由得在处有极值

                               ①

又在处的切线的倾斜角为

          ②

由式①、式②解得

设的方程为

∵原点到直线的距离为，

解得．

又不过第四象限，．

所以切线的方程为．

切点坐标为（2，3），则，

解得

．

（2）

       在上递增，在上递减

       而

       在区间上的最大值是3，最小值是