题目列表(包括答案和解析)
| A、1个 | B、2个 | C、3个 | D、4个 |
对于任意正整数n，定义“n的双阶乘n!!”如下：
当n是偶数时，n!!=n·(n-2)·(n-4)……6·4·2；
当n是奇数时，n!!=n·(n-2)·(n-4)……5·3·1
现在有如下四个命题：①(2003!!)·(2002!!)=2003!；②2002!!=21001·1001!；
③2002!!的个位数是0； ④2003!!的个位数是5.
其中正确的命题有( )
（A）4个 （B）3个 （C）2个 （D）1个
对于任意正整数n，定义“
”如下：
当n是偶数时，
，
当n是奇数时，
现在有如下四个命题：
①
；
②
；
③
的个位数是0；
④
的个位数是5。
其中正确的命题有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
”如下：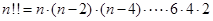
，
；
；
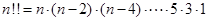
的个位数是0；
的个位数是5。| A．1个 | B．2个 | C．3个 | D．4个 |
| A．10个 | B．15个 | C．16个 | D．18个 |
说明：
一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则.
二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分.
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数.
四、只给整数分数，选择题和填空题不给中间分.
一、选择题：本题考查基本知识和基本运算，每小题5分，满分50分.
1. B 2. C 3. B 4.C 5.D 6.A 7. B 8. A 9. C 10. C
二、填空题：本题考查基本知识和基本运算，每小题4分，满分20分.
11. 1 12. 
13.
2 14. 
15.
①③
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤.
16. 本题主要考查三角函数的倍角公式、两角和公式等基本知识，考查学生的运算求解能
力. 满分13分.
解：（Ⅰ）因为
，
两边同时平方得
.
………………………………………（4分）
又
，
所以
.
………………………………………（6分）
（Ⅱ）因为，
，
所以
，得
.
又
,知
. …………………（9分）
. ………………………………………（13分）
17. 本题主要考查线线位置关系，二面角的求法等基本知识，考查空间想像能力，运算求解能力和推理论证能力. 满分13分.
解：（Ⅰ）证明：连结
，
侧棱
底面ABC，
，又
.
平面
.
又
平面，
. ………（3分）
，
四边形为正方形，
.
， 
平面
.
又
平面，
. …………（6分）
（Ⅱ）
.
平面
.
又
， 
.
如图，以
为原点，建立空间直角坐标系-xyz，设AP=x，则
、
、
、
.
知面
的一个法向量为
， ……（9分）
设面
的一个法向量为
，
，
.
由
得
令
， 
………（11分）
依题意：
=
解得
（不合题意，舍去），
时，二面角
的大小为
. …………（13分）
18．本题主要考查数列与不等式等基本知识，考查运用数学知识分析问题与解决问题的能力，
考查应用意识. 满分13分.
解：设第一年（今年）的汽车总量为
，第n年的汽车总量为
，则
，
…
.
数列
构成的首项为80000，公差为2000的等差数列，
. ………………………（4分）
若洗车行A从今年开始经过n年可以收回购买净化设备的成本. 则（
）
-20000n≥900000，………………………（8分）
整理得，
因为
，所以 
.
答：至少要经过6年才能收回成本. …………………………………………（13分）
19．本题主要考查直线与抛物线的位置关系、等比数列求和等基本知识，考查运算求解能力和分析问题、解决问题的能力. 满分13分
解：（Ⅰ）依题意得：
，解得
.
所以抛物线方程为
. ………………………………………………（3分）
（Ⅱ）若
，即直线AB垂直于x轴，不防设
，
由
又由抛物线对称性可得：
.
又
，得 
，故S△ABD=
. …………………………（4分）
若
，设直线AB方程：
，
由方程组
消去
得：
.（※）
依题意可知：
.
由已知得
，
. ……………………………………（5分）
由
，得
，
即
，整理得
.
所以
. …………………………………………（6分）
中点
，
所以点
，
依题意知
.
又因为方程（※）中判别式
，得
.
所以
，又
，
所以
.
又
为常数，故
的面积为定值. …………………………………（9分）
（Ⅲ）依题意得：
…，
.
故
…
＜
. ………………………………（13分）
注：本题第（Ⅱ）问另解，参照本标准给分；第（Ⅲ）问若用定积分证明，同样给分.
20. 本题主要考查函数的单调性、极值、最值、不等式等基本知识，考查运用导数研究函数
性质的方法，考查分类与整合及化归与转化等数学思想. 满分14分.
解：（Ⅰ）依题意，知
的定义域为
.
当
时，
，
.
令
，解得
.
当
时，
；当
时，
.
又
，
所以的极小值为
，无极大值 . …………………………（3分）
（Ⅱ）
.
令，解得
. …………………………（4分）
若
，令，得；令，得 .
若
，
①当
时，
，
令，得
或；
令，得
.
②当
时，
.
③当
时，得
，
令，得或
；
令，得
.
综上所述，当时，的递减区间为
，递增区间为
.
当
时，的递减区间为
；递增区间为
.
当时，递减区间为.当时，的递减区间为
，递增区间为
. …………………………（9分）
（Ⅲ）当
时，
，
由
，知
时，
. 
，
.
依题意得：
对一切正整数成立. ……………（11分）
令
，则
（当且仅当
时取等号）.
又
在区间
单调递增，得
，
故
，又
为正整数，得
，
当
时，存在
，
，
对所有
满足条件.
所以，正整数的最大值为32. …………………………………（14分）
21. （1）本题主要考查矩阵乘法与变换等基本知识，考查运算求解能力，考查函数与方程思
想. 满分7分.
解：PQ＝
，
PQ矩阵表示的变换T：
满足条件
.
所以
………………………（3分）
直线
任取点
，则点
在直线
上，
故
，又，得
所以
………………………………………（7分）
（2）本题主要考查直线极坐标方程和椭圆参数方程等基本知识，考查运算求解能力，考查化归与转化思想. 满分7分.
解：由题意知直线和椭圆方程可化为：
， ①
． ② …………………………（２分）
①②联立，消去
得：
，解得
，
．
设直线与椭圆交于A、B两点，则
．
故所求的弦长为
． &n
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com