
题目列表(包括答案和解析)
 如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.| dm |
| N△? |
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置。将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀。将试测线圈引线的两端与冲击电流计D相连。拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转。

(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度为Dφ, Dφ=![]() ,式中
,式中![]() 为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B= ;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε= 。
为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B= ;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε= 。
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表。由此可得,螺线管A内部在感应强度B和电流I的关系为B= 。
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
(3)(多选题)为了减小实验误差,提高测量的准确性,可采取的措施有
(A)适当增加试测线圈的匝数N
(B)适当增大试测线圈的横截面积S
(C)适当增大可变电阻R的阻值
(D)适当拨长拨动开关的时间Δt
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置。将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀。将试测线圈引线的两端与冲击电流计D相连。拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转。
(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度为Dφ, Dφ=![]() ,式中
,式中![]() 为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B=______;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε=____。
为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B=______;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε=____。
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表。由此可得,螺线管A内部在感应强度B和电流I的关系为B=______。
(3)为了减小实验误差,提高测量的准确性,可采取的措施有( )
A.适当增加试测线圈的匝数N B.适当增大试测线圈的横截面积S
C.适当增大可变电阻R的阻值 D.适当拨长拨动开关的时间Δt
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
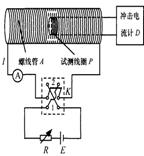
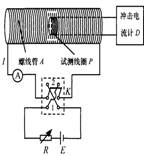 如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置。将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀。将试测线圈引线的两端与冲击电流计D相连。拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转。
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置。将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀。将试测线圈引线的两端与冲击电流计D相连。拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转。
(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度为Dφ, Dφ=![]() ,式中
,式中![]() 为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B=______;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε=____。
为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B=______;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε=____。
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表。由此可得,螺线管A内部在感应强度B和电流I的关系为B=______。
(3)(多选题)为了减小实验误差,提高测量的准确性,可采取的措施有( )
A.适当增加试测线圈的匝数N B.适当增大试测线圈的横截面积S
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
C.适当增大可变电阻R的阻值 D.适当拨长拨动开关的时间Δt
(10分)如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置。将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀。将试测线圈引线的两端与冲击电流计D相连。拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转。
(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度为Dφ,Dφ= ,式中
,式中 为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B= ;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε= 。
为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度B= ;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势ε= 。
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表。由此可得,螺线管A内部在感应强度B和电流I的关系为B= 。
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
高考真题
1.【解析】对A选项,静止的导线上的稳恒电流附近产生稳定的磁场,通过旁边静止的线圈不会产生感应电流,A被否定;稳恒电流周围的稳定磁场是非匀强磁场,运动的线圈可能会产生感应电流,B符合事实;静止的磁铁周围存在稳定的磁场,旁边运动的导体棒会产生感应电动势,C符合;运动的导线上的稳恒电流周围产生运动的磁场,即周围磁场变化,在旁边的线圈中产生感应电流,D符合。
【答案】A
2.【解析】本题考查右手定则的应用。根据右手定则,可判断PQ作为电源,Q端电势高,在PQcd回路中,电流为逆时针方向,即流过R的电流为由c到d,在电阻r的回路中,电流为顺时针方向,即流过r的电流为由b到a。当然也可以用楞次定律,通过回路的磁通量的变化判断电流方向.所以选项B正确
【答案】B
3.【解析】如图所示,设观察方向为面向北方,左西右东,则地磁场方向平行赤道表面向北,
电磁感应.files/image211.gif) 若飞机由东向西飞行时,由右手定则可判断出电动势方向为由上
若飞机由东向西飞行时,由右手定则可判断出电动势方向为由上
向下,若飞机由西向东飞行时,由右手定则可判断出电动势方向
为由下向上,A对B错;沿着经过地磁极的那条经线运动时,速
度方向平行于磁场,金属杆中一定没有感应电动势,C错D对。
【答案】AD
4.【解析】在释放的瞬间,速度为零,不受安培力的作用,只受到重力,A对。由右手定则可得,电流的方向从b到a,B错。当速度为电磁感应.files/image213.gif) 时,产生的电动势为
时,产生的电动势为电磁感应.files/image215.gif) ,受到的安培力为
,受到的安培力为电磁感应.files/image217.gif) ,计算可得
,计算可得电磁感应.files/image219.gif) ,C对。在运动的过程中,是弹簧的弹性势能、重力势能和内能的转化,D错。
,C对。在运动的过程中,是弹簧的弹性势能、重力势能和内能的转化,D错。
【答案】AC
5.【解析】在x=R左侧,设导体棒与圆的交点和圆心的连线与x轴正方向成θ角,则导体棒切割有效长度L=2Rsinθ,电动势与有效长度成正比,故在x=R左侧,电动势与x的关系为正弦图像关系,由对称性可知在x=R右侧与左侧的图像对称。
【答案】A
6.【解析】考查自感现象。电键K闭合时,电感L1和L2的电流均等于三个灯泡的电流,断开电键K的瞬间,电感上的电流i突然减小,三个灯泡均处于回路中,故b、c灯泡由电流i逐渐减小,B、C均错,D对;原来每个电感线圈产生感应电动势均加载于灯泡a上,故灯泡a先变亮,然后逐渐变暗,A对。本题涉及到自感现象中的“亮一下”现象,平时要注意透彻理解。
【答案】AD.
7.【解析】该题利用导体在磁场中的切割模型综合考查法拉第电磁感应定律、欧姆定律、物体平衡、牛顿第二定律和变速直线运动规律;导体从静止开始又变加速到匀加速,又由匀加速到匀速直至完成全过程,环环相扣,逐步深入,循序渐进,无不渗透着经典物理的科学思想和方法.
(1)体棒ab从A处下落时的有效切割长度为电磁感应.files/image221.gif) r,由法拉第电磁感应定律得:
r,由法拉第电磁感应定律得:
E1=电磁感应.files/image223.gif) Brv1,此时等效电路的电阻为R总1==4R,所以I1==,故安培力F1=BI
Brv1,此时等效电路的电阻为R总1==4R,所以I1==,故安培力F1=BI
(2)有效切割长度为2r,所以感应电动势为E2=2Brv,此时等效电路的电阻为R总2==3R,所以I2==,故安培力为F2=BI2L2=,因棒中电流大小始终不变,也就是速度不变,所以棒受力平衡,即mg=,v=,在无磁场区域棒做匀加速直线运动,由匀变速直线运动规律v2-v22=2gh,所以h=-,得I22=I2=,故P2=I222R2==,
(3)由牛顿第二定律F+mg-=ma,所以F=ma-mg+
【答案】(1) a=g- (2) (3) F=ma-mg+
8.(1)a和b不受安培力作用,由机械能守恒可知电磁感应.files/image225.gif)
(2)设导体棒刚进入无磁场区域时的速度为电磁感应.files/image227.gif) ,刚离开无磁场区域时的速度为
,刚离开无磁场区域时的速度为电磁感应.files/image229.gif) ,
,
由能量守恒得:在磁场区域中,电磁感应.files/image231.gif)
在无磁场区域中,电磁感应.files/image233.gif)
解得:电磁感应.files/image235.gif)
(3)在无磁场区域,根据匀变速直线运动规律电磁感应.files/image237.gif) ,且平均速度
,且平均速度电磁感应.files/image239.gif) ,有磁场区域,棒a受到的合力
,有磁场区域,棒a受到的合力电磁感应.files/image241.gif)
感应电动势电磁感应.files/image215.gif) ,感应电流
,感应电流电磁感应.files/image244.gif) ,解得
,解得电磁感应.files/image246.gif)
根据牛顿第二定律,在t到电磁感应.files/image248.gif) 时间内
时间内电磁感应.files/image250.gif)
电磁感应.files/image252.gif)
解得电磁感应.files/image254.gif)
【答案】(1)电磁感应.files/image225.gif)
(2) 电磁感应.files/image235.gif)
(3)电磁感应.files/image254.gif)
9.【解析】(1)改变电流方向,磁通量变化量为原来磁通量的两倍,即2BS,代入公式计算得B=电磁感应.files/image256.gif) ,由法拉第电磁感应定律可知电动势的平均值ε=
,由法拉第电磁感应定律可知电动势的平均值ε=电磁感应.files/image258.gif) 。
。
(2)根据数据可得B与I成正比,比例常数约为0.00125,故B=kI(或0.00125I)
(3)为了得到平均电动势的准确值,时间要尽量小,由B的计算值可看出与N和S相关联,故选择A、B。
【答案】(1)电磁感应.files/image256.gif) ,
,电磁感应.files/image258.gif)
(2)0.00125I(或kI)
(3)A,B
10.【解析】正确分析线框的受力情况和运动情况是解决问题的关键
(1)cd边刚进入磁场时,做自由落体运动,线框速度v=电磁感应.files/image260.gif)
所以线框中产生的感应电动势E=BLv=BL电磁感应.files/image260.gif)
(2)电磁感应.files/image262.gif) 此时线框中电流 I=
此时线框中电流 I=电磁感应.files/image264.gif)
电磁感应.files/image262.gif) 由分压原理可得,cd两点间的电势差U=I(
由分压原理可得,cd两点间的电势差U=I(电磁感应.files/image267.gif) )=
)=电磁感应.files/image269.gif)
(3)安培力 F=BIL=电磁感应.files/image271.gif) 根据牛顿第二定律mg-F=ma,由a=0
根据牛顿第二定律mg-F=ma,由a=0
解得下落高度满足 h=电磁感应.files/image273.gif)
【答案】(1)E=BLv=BL电磁感应.files/image260.gif) (2)U=I(
(2)U=I(电磁感应.files/image267.gif) )=
)=电磁感应.files/image269.gif) (3)
(3)电磁感应.files/image273.gif)
11.【解析】导体棒所受的安培力为:F=BIl………………①
由题意可知,该力的大小不变,棒做匀减速运动,因此在棒的速度从v0减小到v1的过程中,平均速度为:电磁感应.files/image275.gif) ……………………②
……………………②
当棒的速度为v时,感应电动势的大小为:E=Blv………………③
棒中的平均感应电动势为:电磁感应.files/image277.gif) ………………④
………………④
综合②④式可得:电磁感应.files/image279.gif) ………………⑤
………………⑤
导体棒中消耗的热功率为:电磁感应.files/image281.gif) ………………⑥
………………⑥
负载电阻上消耗的热功率为:电磁感应.files/image283.gif) …………⑦
…………⑦
由以上三式可得:电磁感应.files/image285.gif) …………⑧
…………⑧
【答案】(1) 电磁感应.files/image279.gif) (2)
(2)电磁感应.files/image285.gif)
12.【解析】(1)由于列车速度与磁场平移速度不同,导致穿过金属框的磁通量发生变化,由于电磁感应,金属框中会产生感应电流,该电流受到的安培力即为驱动力。
(2)为使列车获得最大驱动力,MN、PQ应位于磁场中磁感应强度同为最大值且反向的地方,这会使得金属框所围面积的磁通量变化率最大,导致框中电流最强,也会使得金属框长边中电流受到的安培力最大。因此,d应为电磁感应.files/image287.gif) 的奇数倍,即
的奇数倍,即
电磁感应.files/image289.gif) 或
或电磁感应.files/image291.gif) (
(电磁感应.files/image293.gif) )①
)①
(3)由于满足第(2)问条件:则MN、PQ边所在处的磁感应强度大小均为B0且方向总相反,经短暂的时间电磁感应.files/image295.gif) ,磁场沿Ox方向平移的距离为
,磁场沿Ox方向平移的距离为电磁感应.files/image297.gif) ,同时,金属框沿Ox方向移动的距离为
,同时,金属框沿Ox方向移动的距离为电磁感应.files/image299.gif) 。 因为v0>V,所以在
。 因为v0>V,所以在电磁感应.files/image295.gif) 时间内MN边扫过磁场的面积
时间内MN边扫过磁场的面积电磁感应.files/image301.gif)
在此电磁感应.files/image295.gif) 时间内,MN边左侧穿过S的磁通移进金属框而引起框内磁通量变化
时间内,MN边左侧穿过S的磁通移进金属框而引起框内磁通量变化
电磁感应.files/image303.gif)
同理,该电磁感应.files/image295.gif) 时间内,PQ边左侧移出金属框的磁通引起框内磁通量变化
时间内,PQ边左侧移出金属框的磁通引起框内磁通量变化
电磁感应.files/image305.gif)
故在电磁感应.files/image295.gif) 内金属框所围面积的磁通量变化
内金属框所围面积的磁通量变化电磁感应.files/image307.gif)
根据法拉第电磁感应定律,金属框中的感应电动势大小 电磁感应.files/image309.gif)
根据闭合电路欧姆定律 电磁感应.files/image311.gif)
根据安培力公式,MN边所受的安培力电磁感应.files/image313.gif) PQ边所受的安培力
PQ边所受的安培力 电磁感应.files/image315.gif)
根据左手定则,MN、PQ边所受的安培力方向相同,此时列车驱动力的大小
电磁感应.files/image317.gif) 联立解得
联立解得 电磁感应.files/image319.gif)
【答案】(1) 电流受到的安培力即为驱动力 (2) 电磁感应.files/image289.gif) (3)
(3)电磁感应.files/image319.gif)
名校试题
1.【解析】若保持电键闭合,磁通量不变,感应电流消失,所以铝环跳起到某一高度后将回落;正、负极对调,同样磁通量增加,由楞次定律,铝环向上跳起.
【答案】CD
2.【解析】 是楞次定律可以判断选项AC正确
【答案】AC
3.【解析】橡胶盘A在加速转动时,产生的磁场在不断增加,穿过B的磁通量不断增加,根据楞次定律可知B正确。
【答案】B
4.【解析】矩形线框向上进入匀强磁场时,受到向下的重力和磁场力,致使速度减小,所
以v1>v2,A正确;进入磁场后上升阶段从位置2到位置3,无磁场力,重力做负功,所以v2>v3,B错误;从位置2上升至最高点后再返回至位置2,无磁场力,重力做功为零,所以v2=v4,C正确;下落离开磁场的过程中,受到向下的重力和向上的磁场力,两个力大小无法确定,所以v4与v5无法比较,D错误。
【答案】AC
5.【解析】当拉力恒定时,电磁感应.files/image321.gif)
最终以电磁感应.files/image049.gif) 的速度做匀速运动,则
的速度做匀速运动,则电磁感应.files/image324.gif) ,代入
,代入电磁感应.files/image047.gif) 的表达式中得
的表达式中得电磁感应.files/image327.gif)
当功率恒定时,电磁感应.files/image329.gif)
最终以电磁感应.files/image049.gif) 的速度做匀速运动,则
的速度做匀速运动,则电磁感应.files/image332.gif)
代入电磁感应.files/image334.gif) 的表达式中得
的表达式中得电磁感应.files/image336.gif)
电磁感应.files/image337.jpg) 【答案】C
【答案】C
6.【解析】对电磁感应.files/image064.gif) 、
、电磁感应.files/image066.gif) 棒受力分析如图所示,从能的转化与守恒角度出发,可推知外力F克服
棒受力分析如图所示,从能的转化与守恒角度出发,可推知外力F克服电磁感应.files/image064.gif) 棒所受的摩擦力
棒所受的摩擦力电磁感应.files/image340.gif) 做功直接将其他形式的能转化为内能,而F克服安培阻力
做功直接将其他形式的能转化为内能,而F克服安培阻力电磁感应.files/image342.gif) 做的功将其他形式的能转化为电能,其功率为P电=(F-f)Va,故感应电流做功的
功率也为
做的功将其他形式的能转化为电能,其功率为P电=(F-f)Va,故感应电流做功的
功率也为电磁感应.files/image078.gif) ,C项正确.本题易错选D,实际上它是回路的总电能的一部分。在
,C项正确.本题易错选D,实际上它是回路的总电能的一部分。在电磁感应.files/image066.gif) 棒上通过
棒上通过电磁感应.files/image345.gif) 克服
克服电磁感应.files/image347.gif) 做功转化为
做功转化为电磁感应.files/image066.gif) 棒与轨道的内能,功率
棒与轨道的内能,功率电磁感应.files/image350.gif) .这时
.这时电磁感应.files/image066.gif) 棒与相当于电动机通过感应电流而运动,把电能通过克服
棒与相当于电动机通过感应电流而运动,把电能通过克服电磁感应.files/image347.gif) 做功转化为内能.电能的另一部分,由电流的热效应转化为电路的内能,电能的另一部分,由电流的热效应转化为电路的内能,其功率为感应电流做功的总功率减去
做功转化为内能.电能的另一部分,由电流的热效应转化为电路的内能,电能的另一部分,由电流的热效应转化为电路的内能,其功率为感应电流做功的总功率减去电磁感应.files/image066.gif) 棒上输出的功率,即
棒上输出的功率,即电磁感应.files/image355.gif) ,故D项所指正是这部分功率而非感应电流做功的总功率.
,故D项所指正是这部分功率而非感应电流做功的总功率.
【答案】C
7.【解析】⑴匀速时,拉力与安培力平衡,F=BIL
得:电磁感应.files/image357.gif)
⑵金属棒a切割磁感线,产生的电动势E=BLv
回路电流电磁感应.files/image244.gif) 联立得:
联立得:电磁感应.files/image360.gif)
⑶平衡时,棒和圆心的连线与竖直方向的夹角为θ,
电磁感应.files/image362.gif) 得:θ=60°
得:θ=60°
电磁感应.files/image364.gif)
【答案】(1)电磁感应.files/image357.gif) (2)
(2)电磁感应.files/image360.gif) (3)
(3)电磁感应.files/image364.gif)
8.【解析】(1)设ab棒离开磁场边界前做匀速运动的速度为v,产生的电动势为E = BLv…
电路中电流 I = 电磁感应.files/image366.gif) ……………对ab棒,由平衡条件得 mg-BIL = 0…
……………对ab棒,由平衡条件得 mg-BIL = 0…
解得 v = 电磁感应.files/image368.gif)
(2) 由能量守恒定律:mg(d0 + d) = E电 + 电磁感应.files/image370.gif) mv2
mv2
解得 电磁感应.files/image372.gif) ,
,电磁感应.files/image374.gif)
(3)设棒刚进入磁场时的速度为v0,由mgd0 = 电磁感应.files/image370.gif) mv02,得v0 =
mv02,得v0 = 电磁感应.files/image377.gif)
棒在磁场中匀速时速度为v = 电磁感应.files/image368.gif) ,则
,则
1 当v0=v,即d0 = 电磁感应.files/image379.gif) 时,棒进入磁场后做匀速直线运
时,棒进入磁场后做匀速直线运
2 当v0 < v,即d0 <电磁感应.files/image379.gif) 时,棒进入磁场后做先加速后匀速直线运动
时,棒进入磁场后做先加速后匀速直线运动
3 当v0>v,即d0>电磁感应.files/image379.gif) 时,棒进入磁场后做先减速后匀速直线运动
时,棒进入磁场后做先减速后匀速直线运动
【答案】(1)电磁感应.files/image368.gif) (2)
(2)电磁感应.files/image374.gif) (3)
(3)电磁感应.files/image368.gif)
9.【解析】(1)电磁感应.files/image383.gif) 匀速下降时,金属杆匀速上升,回路中产生的感应电动势为:
匀速下降时,金属杆匀速上升,回路中产生的感应电动势为:电磁感应.files/image385.gif)
则电磁感应.files/image387.gif)
对电磁感应.files/image383.gif) 、
、电磁感应.files/image098.gif) 整体有:
整体有:电磁感应.files/image391.gif)
由以上式子解得:电磁感应.files/image393.gif)
(2)由(1)得:电磁感应.files/image395.gif)
由电磁感应.files/image101.gif) 图象可知:
图象可知:电磁感应.files/image398.gif)
所以解得:电磁感应.files/image400.gif)
【答案】(1) 电磁感应.files/image393.gif) (2)
(2)电磁感应.files/image400.gif)
10.【解析】(1)当金属棒匀速下滑时速度最大,设最大速度为vm,达到最大时则有
mgsinθ=F安 F安=ILB
电磁感应.files/image402.gif) 其中 R总=6R
所以
mgsinθ=
其中 R总=6R
所以
mgsinθ=电磁感应.files/image404.gif) 解得最大速度
解得最大速度 电磁感应.files/image406.gif)
(2)R2上消耗的功率 电磁感应.files/image408.gif) 其中
其中 电磁感应.files/image410.gif)
电磁感应.files/image412.gif) 又
又 电磁感应.files/image414.gif)
解以上方程组可得电磁感应.files/image416.gif)
当电磁感应.files/image418.gif) 时,R2消耗的功率最大
最大功率
时,R2消耗的功率最大
最大功率电磁感应.files/image420.gif)
【答案】(1)电磁感应.files/image406.gif) (2)
(2) 电磁感应.files/image420.gif)
11.【解析】(1)在t=0至t=4s内,金属棒PQ保持静止,磁场变化导致电路中产生感应电动势.电路为r与R并联,再与RL串联,电路的总电阻
电磁感应.files/image422.gif) =5Ω
①
=5Ω
①
此时感应电动势
电磁感应.files/image424.gif) =0.5×2×0.5V=0.5V
②
=0.5×2×0.5V=0.5V
②
通过小灯泡的电流为:电磁感应.files/image426.gif) =0.1A
③
=0.1A
③
(2)当棒在磁场区域中运动时,由导体棒切割磁感线产生电动势,电路为R与RL并联,再与r串联,此时电路的总电阻
电磁感应.files/image428.gif) =2+Ω=Ω ④
=2+Ω=Ω ④
由于灯泡中电流不变,所以灯泡的电流IL=0.1A,则流过棒的电流为
电磁感应.files/image430.gif) =
=
电动势电磁感应.files/image432.gif) ⑥
⑥
解得棒PQ在磁场区域中v=1m/s
【答案】(1) 0.1A (2)运动的速度大小v=1m/s
12.【解析】(1)ab杆向右运动时,ab杆中产生的感应电动势方向为a→b,大小为E=BLv1,… 耐杆中的感应电流方向为d→c.cd杆受到的安培力方向水平向右
安培力大小为电磁感应.files/image434.gif) ①
①
解①、③两式,ab杆匀速运动的速度为电磁感应.files/image436.gif) ③
③
(2)ab杆所受拉力F=电磁感应.files/image438.gif) ④
④
(3)设cd杆以v2速度向下运动h过程中,ab杆匀速运动了s距离
电磁感应.files/image440.gif)
整个回路中产生的焦耳热等于克服安培力所做的功
电磁感应.files/image442.gif) …
…
【答案】(1) 电磁感应.files/image436.gif) (2
(2电磁感应.files/image438.gif) ) (3)
) (3)电磁感应.files/image442.gif)
13.【解析】导轨在外力作用下向左加速运动,由于切割磁感线,在回路中要产生感应电流,导轨的bc边及金属棒PQ均要受到安培力作用PQ棒受到的支持力要随电流的变化而变化,导轨受到PQ棒的摩擦力也要变化,因此导轨的加速度要发生改变.导轨向左切割磁感线时,感应电动势 E=BLv ①
感应电流 电磁感应.files/image444.gif) ②
②
即电磁感应.files/image446.gif) ③ 导轨受到向右的安培力F 1= BIL,金属棒PQ受到向上的安培力F2= BIL,导轨受到PQ棒对它的摩擦力
③ 导轨受到向右的安培力F 1= BIL,金属棒PQ受到向上的安培力F2= BIL,导轨受到PQ棒对它的摩擦力电磁感应.files/image448.gif) ,
,
根据牛顿第二定律,有
电磁感应.files/image450.gif) ④
④
(1)当刚拉动导轨时,v=0,由③④式可知I=0时有最大加速度am,即
电磁感应.files/image452.gif) m/s2
m/s2
(2)随着导轨速度v增大感应电流I增大而加速度a减小,当a=0时,导轨有最大速度vm,从④式可得
电磁感应.files/image454.jpg)
电磁感应.files/image456.gif)
电磁感应.files/image458.gif) A
A
将电磁感应.files/image460.gif) A代入③式,得
A代入③式,得
电磁感应.files/image462.gif) m/s
m/s
|