
题目列表(包括答案和解析)
(8分)如图,一透明球体置于空气中,球半径R=10cm,折射率n=![]() .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点, AB与MN间距为
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点, AB与MN间距为![]() cm
cm
⑴补全光路并求出光从B点传到C点的时间;(真空中光速c=3×108m/s)
⑵求CD与MN所成的角α.(需写出求解过程)

(10分)如图,一透明球体置于空气中,球半径R=10cm,折射率n=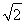 .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5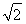 cm,CD为出射光线.
cm,CD为出射光线.
(1)补全光路并求出光从B点传到C点的时间;
(2)求CD与MN所成的角α.(写出求解过程)
(10分)如图,一透明球体置于空气中,球半径R=10cm,折射率n= .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5 cm,CD为出射光线.
cm,CD为出射光线.
(1)补全光路并求出光从B点传到C点的时间;
(2)求CD与MN所成的角α.(写出求解过程)
 .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5 cm,CD为出射光线.
cm,CD为出射光线.
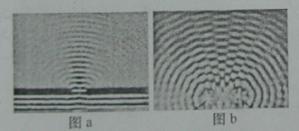
(1)利用发波水槽得到的水面波形如a,b所示,则 ( )
A.图a、b均显示了波的干涉现象
B.图a、b均显示了波的衍射现象
C.图a显示了波的干涉现象,图b显示了波的衍射现象
D.图a显示了波的衍射现象,图b显示了波的干涉现象
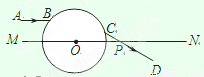
(2)如图所示,一透明球体置于空气中,球半径R=10cm,折射率n=![]() .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点, AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点, AB与MN间距为5![]() cm,CD为出射光线。
cm,CD为出射光线。
①补全光路并求出光从B点传到C点的时间;
②求CD与MN所成的角α.(需写出求解过程)

高考真题
1.【解析】通过手指的缝隙观察日光灯,看到彩色条纹,是光的衍射现象。D不正确。
光%20%20%20%20学.files/image097.gif) 【答案】D
【答案】D
2.【解析】由题可知单色光在玻璃球体发生了全反射,如图24所示,
为光线在玻璃球内的光路图.A、C为折射点,B为反射点,作OD
平行于入射光线,故光%20%20%20%20学.files/image099.gif) ,所以
,所以光%20%20%20%20学.files/image101.gif) ,
,
玻璃的折射率光%20%20%20%20学.files/image103.gif) .
.
【答案】C 图24
3.【解析】依题意,画出红、蓝光线经过平板玻璃砖实的光路如图25示。玻璃中的光速则为光%20%20%20%20学.files/image105.gif) ,设玻璃砖的厚度为d,在未发生全反射之前,光通过玻璃砖的时间为
,设玻璃砖的厚度为d,在未发生全反射之前,光通过玻璃砖的时间为光%20%20%20%20学.files/image106.gif)
光%20%20%20%20学.files/image108.gif) 。由折射定律知
。由折射定律知光%20%20%20%20学.files/image110.gif) ,因此,
,因此,光%20%20%20%20学.files/image112.gif) ,由于蓝光的频率大于红光的频率,故玻璃对红光的折射率n1小于对蓝光的折射率n2且都大于1.5,考虑以上因素,
,由于蓝光的频率大于红光的频率,故玻璃对红光的折射率n1小于对蓝光的折射率n2且都大于1.5,考虑以上因素,
图25
由此式可知,在未发生全反射之前,t1<t2。
【答案】B
4.【解析】白光作杨氏双缝干涉实验,屏上将呈现彩色条纹,A错;用红光作光源,屏上将呈现红色两条纹与暗条纹(即黑条纹)相间,B对;红光和紫光频率不同,不能产生干涉条纹,C错;紫光作光源,遮住一条狭缝,屏上出现单缝衍射条纹,即间距不等的条纹,D对
【答案】BD
5.【解析】金属丝圈的转动,改变不了肥皂液膜的上薄下厚的形状,由干涉原理可知干涉条纹与金属丝圈在该竖直平面内的转动无关,仍然是水平的干涉条纹,D对。 图4
【答案】D
6.【解析】吹出的肥皂泡却是彩色的,证时了光的干涉现象,热中子的德布罗意波长与晶体中原子间距大致相同,说明了光的波动性.
【答案】BD
7.【解析】微波是电磁波,其波长在10-3m到10m之间;黑体的热辐射是辐射电磁波;普朗克在研究黑体的热辐射问题中提出了能量子假说
【答案】ACD
8.【解析】光导纤维传递光信号的是利用了几何光学的全反射 ,全反射的条件是光从光密介质射向光疏介质,且入射角等于或大于临界角
【答案】全反射 光疏介质 临界角
9.【解析】设入射光线与1/4球体的交点为C,连接OC,OC即为 光%20%20%20%20学.files/image114.jpg) 入射点的法线。因此,图中的角α为入射角。过C点作球体水平表面的垂线,垂足为B。依题意,∠COB=α。又由△OBC知sinα=
入射点的法线。因此,图中的角α为入射角。过C点作球体水平表面的垂线,垂足为B。依题意,∠COB=α。又由△OBC知sinα=光%20%20%20%20学.files/image116.gif) 设光线在C点的折射角为β,
设光线在C点的折射角为β,
由折射定律得光%20%20%20%20学.files/image118.gif)
由以上式得光%20%20%20%20学.files/image120.gif) 图26
图26
由几何关系知,光线在球体的竖直表面上的入射角γ(见图26)为30°。由折射定律得光%20%20%20%20学.files/image122.gif)
光%20%20%20%20学.files/image124.gif) 因此
因此光%20%20%20%20学.files/image126.gif) ,所以
,所以光%20%20%20%20学.files/image122.gif)
光%20%20%20%20学.files/image129.gif)
【答案】光%20%20%20%20学.files/image129.gif)
10.【解析】(1)设光在介质中的传播速度为v,波长为λ,频率为f,则
f=光%20%20%20%20学.files/image131.gif) ①
①
光%20%20%20%20学.files/image133.gif) ②
②
联立①②式得 光%20%20%20%20学.files/image122.gif)
光%20%20%20%20学.files/image136.gif) ③
③
从波形图上读出波长光%20%20%20%20学.files/image138.gif) m,代入数据解得
m,代入数据解得
f=5×1014Hz
光%20%20%20%20学.files/image139.jpg) 根据光线a在AC面的的入射角和折射角知玻璃砖的折射率
根据光线a在AC面的的入射角和折射角知玻璃砖的折射率光%20%20%20%20学.files/image141.gif) ,设此玻璃砖的临界角为
,设此玻璃砖的临界角为光%20%20%20%20学.files/image143.gif) ,解得
,解得光%20%20%20%20学.files/image145.gif) ,光线b在CD面上入射角和几何关系可知为
,光线b在CD面上入射角和几何关系可知为光%20%20%20%20学.files/image147.gif) ,因为
,因为光%20%20%20%20学.files/image147.gif)
光%20%20%20%20学.files/image149.gif)
光%20%20%20%20学.files/image151.gif) ,故b在CD面上反生全反射;射到BD面的入射角由几何关系可知为
,故b在CD面上反生全反射;射到BD面的入射角由几何关系可知为光%20%20%20%20学.files/image153.gif) ,因
,因光%20%20%20%20学.files/image153.gif)
光%20%20%20%20学.files/image155.gif)
光%20%20%20%20学.files/image151.gif) ,故不会发生全反射而从BD面射出.根据折射定律可求得出射光线与界面法线的夹角为
,故不会发生全反射而从BD面射出.根据折射定律可求得出射光线与界面法线的夹角为光%20%20%20%20学.files/image151.gif) ,故上述光路如
,故上述光路如
图27所示。
【答案】(1)f=5×1014Hz(2)图27所示
图27
11光%20%20%20%20学.files/image157.gif) .【解析】当线光源上某一点发出的光线射到未被遮光板遮住的液面上时,射到遮光边缘O的那条光线的入射角最小。如图28所示
.【解析】当线光源上某一点发出的光线射到未被遮光板遮住的液面上时,射到遮光边缘O的那条光线的入射角最小。如图28所示
若线光源底端在A点时,望远镜内刚好可以看到此光源底端,
设过O点液面的法线为OO1,则
光%20%20%20%20学.files/image159.gif) ①
①
其中a为此液体到空气的全反射临界角。由折射定律有
光%20%20%20%20学.files/image161.gif) ②
图28
②
图28
同理,若线光源顶端在B1点时,通过望远镜刚好可以看到此光源顶端,则光%20%20%20%20学.files/image163.gif) 。设此时线光源底端位于B点。由图中几何关系可得
。设此时线光源底端位于B点。由图中几何关系可得
光%20%20%20%20学.files/image165.gif) ③
③
联立②③式得
光%20%20%20%20学.files/image167.gif) ④
④
【答案】光%20%20%20%20学.files/image167.gif)
名校试题
1.【解析】 红光折射率小于蓝光折射率,由折射率公式n=c/v知红光在同种介质中的速度较大,即V1>V2; 由全反射公式sinc=1/n知红光折射率小临界角大; 所以蓝光发生全反射时红光依然有折射现象。选C
【答案】C
2.【解析】由于没有确定几何尺寸,所以光线可能射向Q的右侧面,也可能射向Q的下表面,A错误;当光线射向Q的下表面时,它的入射角与在P中的折射角相等,由于nP<nQ,进入空气中的折射角大于进入P上表面的入射角,那么出射光线与下表面的夹角一定小于θ,B、C错误,D正确。
【答案】D
3.【解析】由能量守恒可知,A正确,B错误;由光子学说及光电效应的规律可知,C错误,D正确。
【答案】AD
4.【解析】两块捏紧的玻璃板表面看到彩色条纹是薄膜干涉,狭缝观察发光的白炽灯也会看到彩色条纹是单缝衍射
【答案】C
5.【解析】单缝衍射的条纹是不等间距,中央亮纹又宽又亮
【答案】D
光%20%20%20%20学.files/image168.gif) 6.【解析】(1)ADEG
6.【解析】(1)ADEG
(2)如图29所示,光%20%20%20%20学.files/image170.gif)
光%20%20%20%20学.files/image172.gif)
x=d(tanr2-tanr1)=d光%20%20%20%20学.files/image174.gif)
【答案】(1)ADEG (2)d光%20%20%20%20学.files/image174.gif)
7.【解析】反射角光%20%20%20%20学.files/image062.gif)
光%20%20%20%20学.files/image177.gif) 60°
③
60°
③
由折射定律
光%20%20%20%20学.files/image179.gif) ④
④
解得折射角r = 30° ⑤
因此反射光束1和透射光束2之间的夹角
光%20%20%20%20学.files/image180.gif)
光%20%20%20%20学.files/image182.gif)
【答案】光%20%20%20%20学.files/image183.gif)
8.【解析】①连接BC,如图30所示
在B点光线的入射角、折射角分别
标为i、r,
Sini=5光%20%20%20%20学.files/image037.gif) /10=
/10=光%20%20%20%20学.files/image037.gif) /2, 所以,
图30
/2, 所以,
图30
i=45°
由折射率定律:
在B点有:光%20%20%20%20学.files/image179.gif)
Sin r=1/2 故:r=30° BC=2Rcos r t= BCn/C=2Rncos r/C
t=(光%20%20%20%20学.files/image186.gif) /3)
×10-9s
/3)
×10-9s
②由几何关系
可知光%20%20%20%20学.files/image188.gif)
光%20%20%20%20学.files/image190.gif) α=30°
α=30°
【答案】(1)t=(光%20%20%20%20学.files/image186.gif) /3)
×10-9s (2)α=30°
/3)
×10-9s (2)α=30°
9.【解析】①P3 应刻的折射率
光%20%20%20%20学.files/image192.gif)
② 最靠近0C边的是紫光;
增大入射角度,紫光在刻度盘上最先消失
【答案】(1)光%20%20%20%20学.files/image194.gif) (2)紫光在刻度盘上最先消失
(2)紫光在刻度盘上最先消失
(3)该束光线第一次从CD面出射时的折射角。
(结果可用三角函数表示)
10.【解析】(1)设光在AD面的入射角、折射角分别为i、r r=30°
根据 光%20%20%20%20学.files/image179.gif)
得 光%20%20%20%20学.files/image197.gif)
(2)根据
光%20%20%20%20学.files/image199.gif)
|