
题目列表(包括答案和解析)
(本小题满分12分)已知函数f(x)=ax+(x≠0,常数a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.
(本小题满分12分) 已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
(本小题满分12分) 已知函数f(x)=loga(1+x),g(x)=loga(1-x),其中(a>0且a≠1),设h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(3)=2,求使h(x)>0成立的x的集合.
(本小题满分12分)
已知函数f(x)=-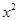 +x+lnx,g(x)=
+x+lnx,g(x)=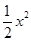 +
+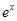 -x
-x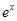 .
.
(Ⅰ)判断函数f(x)的零点的个数,并说明理由;
(Ⅱ)当x∈[-2,2]时,函数g(x)的图像总在直线y=a-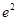 的上方,求实数a的取值范围.
的上方,求实数a的取值范围.
1.C(系数最大项,即是二项式系数最大的项是中间项,2n为偶数,所以中间项为第n+1项,故选C.)2.C(因集合有两个不同的元素,所以方程ax2-2x+1=0有两个不等的解,即 a≠0,Δ=(-2)2-
3.D(由题意可知≠1,解得x≠1,x≠2,故选D)
4.(理)C(∵ =
= =.故选 C.)
(文)B(因为 f′(x)<0(a <x <b),所以函数f(x)在区间(a, b) 是减函数,又f(b)>0,所以函数f(x)在(a,b)内必有f(x)>0.故选B)
5.(理)D(珍藏系列金银、金玉新工艺纪念章和摆件中先去掉一款,分层抽样时每层都是整数,故选D.)
(文)B(∵=,∴12400×=124,故选B.)
6.(理)C(∵f(x) =2x2-lnx的定义域为{x| x>0},又f′(x)=,令f′(x)>0即>0,由定义域为{x| x>0},只须解得x>,因此选C.)
(文)C(因为f(x)=x3+x-2,所以f′(x)=3x2+1.直线y=4x-1的斜率为4,令f′(x)=3x2+1=4,得x=±1,f(1)=0,f(-1)=-4.f(1)=0,f(-1)=-4.所以曲线f(x)=x3+x-2在点(1,0)、(-1,-4)处的切线与直线y=4x-1平行.故选C.)
7.C(当a≠0时,f(x)的图像的对称轴为直线x=1,f(x)=ax2-2ax+c,,∴ a<0,b=-
8.(理)B( 抛掷-次,正好出现2枚正面向上,3枚反面向上的概率为=,Eξ=80×=25,故选B)
(文)D(因为=2,s2=;所以=3-2=4,
S2=9s2=3,故选D)
9.B(令f(x)=x4-4x3-2,则f′(x)=4x3-12x2=4x2(x-3),所以在区间x∈[-1,4],f(x)min=f(3)=-29.即-29>-a,∴a>29,故选 B)
10.C(由题意知p,q中有且仅有一个真命题.
若p真,∵2x-x2=-(x-1)2+1≤1,()x+4>4;∴
1<m≤4,若q真,则7-

11.B(令x=-2即f(2)=f(-2)+f(2),∴f(-2)=0,又f(x)是偶函数,即 f(2)=0,∴f(x+4)=f(x), 故f(x)的周期为4.f(3)=f(-1)=f(1)=2,f(4)=f(0)=0.f(2008)=f(502×4)=f(0)=0.∴f(1)+f(2)+f(3)+… +f(2007)=f(1)+f(2)+f(3)+…+ f (2007)+ f (2008) = 502[f(1)+f(2)+f(3)+f(4)]=2008,故选B.)
12.(理)C(原式可看成点P ( 1, 3 )、Q (-,)两点连线的斜率.令x=-,y=(0≤y≤1);所以x2+y2=1(-1≤x≤0 ) .即点Q位于单位圆在第二象限的圆弧上且端点的坐标分别是B (-1,0)、C (0,1). ∴kPB=;kPC=2,设过点P与圆弧有公共点的直线方程为l:kx-y-k+3=0,则≤1,即k≤.结合图形综上可知:A∈[,2].故选C.)
(文)B(思路一:令x=,y=.则x2+y2=1(x≥0,y≥0).x=sinθ,y=cosθ(0≤θ≤). 所以A=x+y=sinθ+cosθ=sin(θ+) ,又≤θ+≤.则A ∈[1,],故选B.
思路二:A2=1+2=1+2,当m=时,A2最大值为2;当m=1或4时,A2最小值为1.又∵A>0,则A∈[1,],故选B.)
13.(理)0(因为f(x1)=f(x2)=2008,所以x1+x2=-.则f(x1+x2)=0.故答案为0)
(文) (原式=2log32-5log32+2+3log32+=,故答案为 )
14.(理) (首先对这20个数按被3除的余数分类①1,4,7,10,13,16,19.②2,5,8,11,14,17,20.③3,6,9,12,15,18. 故所求的概率是= .故答案为 )
(文)(因为此问题可看成编号为1,2,3,…,n的n个人进行摸奖且每人摸一张, 编号为k的人摸到一号奖券,又每人摸到每一个号的概率相同.故答案为.)
15.300(小于
16.9(因为函数解析式为y=x2且值域为{1,4},所以x=±1,±2.故“同族函数”共有C ?C+
17.解:(1)当 x<0时,-x>0,f(-x)=-(x)2+2(-x)=-x2-2x 1分
又f(x)为奇函数,∴f(-x)=-f(x)=-x2-2x,
∴f(x)=x2+2x,∴m=2,y=f(x)的
图象如右所示 4分

(2)由(1)知
f(x)= ,由图象可知,f(x)在[-1,1]上单调递增,
要使地f(x)在[-1,|a|-2]上单调递增,
只需 8分
解之得-3≤a<-1或1<a≤310分
18.解:(1)因为 f(1)=-3+a(6-a)+b=-a2+
当b ≤-6时,Δ≤0,∴f(1)>0的解集为Φ 4分
当b>-6时,3-<a <3+.
∴f(1)>0的解集为{a|3-<a<3+} 6分
(2)∵ 不等式-3x2+a(6-a)x+b>0的解集为(-1,3)
∴f(x)>0与不等式(x+1)(x-3)<0同解 8分
∵3x2-a(6-a)x-b<0解集为(-1,3) 10分
∴,解之得 12分
19.解:(理)(1)设连对的个数为y,得分为ξ,则y=0,1,2,4
因此ξ的所有可能的取值为0,2,4,8 2分
P(ξ=0)==;P(ξ=2)==;P(ξ=4)==;P(ξ=8)==. 9分
数学?第页(见反面)所以ξ的分布列为
ξ
0
2
4
8
P
10分
(2)Eξ=0×+2×+4×+8×=2
答:该爱好者得分的数学期望为2 12分
(文)(1)抽出的产品中恰有1件正品的可能情况有CC=12种 2分
从这7件产品中一次性随机抽出3件的所有可能有C=35种 4分
则抽出的产品中恰有1件正品数的概率为= ……6分
(2)抽出的产品中正品件数不少于次品件数的可能情况有CC+CC+C=31种 9分
从这7件产品中一次性随机抽出4件的所有可能有C=35种 11分
所以抽出的产品中正品件数不少于次品件数的概率为 12分
20.解:(理)(1)由f(x)=-(x≤-1)得f-1(x)=-(x≤0),an=f-1(an-1)=-. 2分
由a1=-1,得a2=-,a3=-,a4=-,猜想an=-. 4分
①当n=1时,a1=-1=-,猜想成立; 5分
数学?第页②设n=k时猜想成立,即ak=-,当n=k+1时,
ak+1=-=-
=-,即猜想对n=k+1时也成立.
由①、②知,an=-对一切n∈N*成立. ………8分
(2)  =
= =
=
= =-1. 12分
=-1. 12分
(文)(1)由题意得:上年度的利润为(13-10)×5000=15000万元;本年度每辆车的投入成本为10×(1+x);本年度每辆车的出厂价为13×(1+0.7x);本年度年销售量为5000×(1+0.4x),因此本年度的利润为y=[13×(1+0.7x)-10×(1+x)]×5000×(1+0.4x)=(3-0.9x)×5000×(1+0.4x)=-1800x2+1500x+15000(0<x<1),由-1800x2+1500x+15000>15000,解得0<x<,所以当0<x<时,本年度的年利润比上年度有所增加. 5分
(2)本年度的利润为f(x)=(3-0.9x)×3240×(-x2+2x+)=3240×(0.9x3-4.8x2+4.5x+5),则f′(x)=3240×(2.7x2-9.6x+4.5)=972(9x-5)(x-3) 8分
由f′(x)=0,解得x=或x=3,当x∈(0,)时,f′(x)>0,f(x)是增函数;当x∈(,1)时,f′(x)<0,f(x)是减函数. 10分
∴当x=时,f(x)取极大值f()=20000万元,
因为f(x)在(0,1)上只有一个极大值,所以它是最大值,
所以当x=时,本年度的年利润最大,最大利润为20000万元。 12分
21.解:(理)(1)由题设可知,f′(x)=3x2-4ax-
即3+
又3-
∴<a<.故a=1 6分
(2)由题设可知,f(x)=x3-2x2-3x,g(x)=x3+(1+b)x2-b,∴g(x)-f(x)=(b+3)x2+3x-b≥0在区间[-1,2]上恒成立 7分
?)当b+3=0,即b=-3时,g(x)-f(x)=3(x+1)≥0在区间[-1,2]上恒成立. 8分
?)当 b+3≠0,即g(x)-f(x)=(b + 3)x2+3x-b=(b+3)(x + 1)(x-)≥0,在区间[-1,2]上恒成立
①当b+3>0,令 (b + 3)(x + 1)(x - )= 0,解得 x =-1; x =.由题设可知;x=≤-1,即-3<b≤-. 10分
②当b+3<0,令(b + 3)(x + 1)(x-)=0,解得x=-1;x=.由题设可知;x=≥2,即-6≤b<-3 11分
综上可知: 实数b的取值范围是-6≤b≤- ………12分
(文)f′(x)=-3x2+2ax+b, 2分
因为函数f(x)在x=1处的切线斜率为-3,
所以f′(1)=-3+
又f(1)=-1+a+b+c=-2得a+b+c=-1. 2分
(1)函数f(x)在x=-2时有极值,所以f′(-2)=-12-
解得a=-2,b=4,c=-3 5分
所以f(x)=-x3-2x2+4x-3. 6分
(2)因为函数f(x)在区间[-2,0]上单调递增,所以导函数f′(x)=-3x2-bx+b在区间[-2,0]上的值恒大于或等于零, 8分
则,得b≥4, 10分
所以实数b的取值范围为[4+∞). 12分
22.解:(1)①当0≤x≤1时,由2(1-x)≤x 得x≥.∴≤x≤1.
②当1<x≤2时,因x-1≤x 恒成立.∴1<x≤2.
由①②得f(x)≤x 的解集为{x|≤x≤2}. 3分
(2)∵f(0)=2,f(1)=0,f(2)=1,
∴当x=0时,f3(0)=f(f(f(0)))=f(f(2))=f(1)=0;
当 x=1时,f3(1)=f(f(f(1)))=f(f(0))=f(2)=1;
当x=2时,f3(2)=f(f(f(2)))=f(f(1))=f(0)=2.
即对任意x∈A,恒有f3(x)=x. 6分 (8分)
(3)f1()=2(1-)=,f2()=f(f())=f()=,f3()=f(f2())=f()=-1=,f4()=f(f3())=f()=2(1-)=,
一般地,f4k+r()=fr() (k,r∈ N*) ∴ f2007()=f3() = 9分 (12分)
(4)(理)由(1)知,f()=,∴fn()=.则f12()=.∴∈B .
由(2)知,对x=0,或1,或2,恒有f3(x)=x,∴f12(x)=f4×3(x)=x.则0,1,2∈B.
由(3)知,对x=,,,,恒有f12(x)=f4×3(x)=x,∴,,,∈B.
综上所述,,0,1,2, ,,,∈B. ∴B中至少含有8个元素. 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com