
题目列表(包括答案和解析)
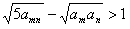 对任何正整数m、n都成立。
对任何正整数m、n都成立。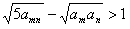 对任何正整数m、n都成立。
对任何正整数m、n都成立。
| |||||||||||||||
(14分)已知在数列{an}中,a1=t,a2=t2,其中t>0,x=![]() 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
(Ⅱ)当![]() 时,令
时,令![]() ,数列
,数列![]() 前
前![]() 项的和为
项的和为![]() ,求证:
,求证:![]()
![]()
(Ⅲ)设![]() ,数列
,数列![]() 前
前![]() 项的和为
项的和为![]() ,
,![]() 求同时满足下列两个条件的
求同时满足下列两个条件的![]() 的值:(1)
的值:(1)![]() (2)对于任意的
(2)对于任意的![]() ,均存在
,均存在![]() ,当
,当![]() 时,
时,![]()
 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式 时,令
时,令 ,数列
,数列 前
前 项的和为
项的和为 ,求证:
,求证:

 ,数列
,数列 前
前 项的和为
项的和为 ,
, 求同时满足下列两个条件的
求同时满足下列两个条件的 的值:(1)
的值:(1) (2)对于任意的
(2)对于任意的 ,均存在
,均存在 ,当
,当 时,
时,

 又在三角形PAC中,E,O分别为PC,AC的中点,
又在三角形PAC中,E,O分别为PC,AC的中点, PA//EO.
PA//EO.
 平面EFOG,PA
平面EFOG,PA 平面EFOG,
平面EFOG,
 PA//平面EFOG,即PA//平面EFG. ………………
PA//平面EFOG,即PA//平面EFG. ………………
…………………………6分
方法二:连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,∴ //
// ,
,
同理 //
//
又 //AB,
//AB, //
// .
.
 平面EFG//平面PAB.
平面EFG//平面PAB.
又PA 平面PAB,
平面PAB, 平面EFG.…………………………………………6分
平面EFG.…………………………………………6分
(2)取AD的中点H,连结GH,则由 知平面EFG即为平面EFHG。
知平面EFG即为平面EFHG。

∴ 的单调减区间为
的单调减区间为 和
和 ,单调增区间为
,单调增区间为 . …………4分
. …………4分
(2)设 ,则
,则 .
.
∴3 =
―3,2
=
―3,2 =6,
=6, =9,即
=9,即 = ―1,
= ―1, =3,
=3, =9.
=9.
故 .
………………………………………………8分
.
………………………………………………8分
由⑴ 知 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
又 >
> =2+
=2+ ,
,
∴ .
.

所以 在
在 上的最小值为
上的最小值为 . ………………………………12分
. ………………………………12分
20.解:(1)由题意知 解得
解得 ,从而
,从而 .
.

21.解:(1)由已知可得 , ∴P是MN的中点,有
, ∴P是MN的中点,有 +
+ =1.
=1.
从而 +
+ =
= +
+ =
=
= 为定值. ………………………………………4分
为定值. ………………………………………4分
(2)由⑴ 知当 +
+ =1时,
=1时, +
+ =
= +
+ =1.
=1.

 +
+ +…+
+…+ ,
①
,
①
又
 +…
+… +
+  ,
②
,
②
① + ② 得 ,故
,故 .…………………………………8分
.…………………………………8分
(3)当 ≥2时,
≥2时, .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com