练习册

  • 练习册
  • 试题
    0．1中年 【查看更多】

     

    题目列表(包括答案和解析)

    中国2010年上海世博会已于2010年5月1日在上海隆重开馆．小王某天乘火车从重庆到上海去参观世博会，若当天从重庆到上海的三列火车正点到达的概率分别为0.8，0.7，0.9，假设这三列火车之间是否正点到达互不影响．求：
    （1）这三列火车恰好有两列正点到达的概率；
    （2）这三列火车至少有一列正点到达的概率．

    查看答案和解析>>

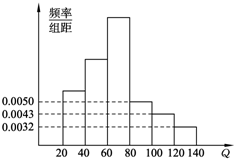    精英家教网中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量Q（简称血酒含量，单位是毫克/100毫升），当20≤Q≤80时，为酒后驾车；当Q＞80时，为醉酒驾车．济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动，共依法查出了60名饮酒后违法驾驶机动车者，如图，为这60名驾驶员抽血检测后所得结果画出的频率分布直方图（其中Q≥140的人数计入120≤Q＜140人数之内）．
    （1）求此次拦查中醉酒驾车的人数；
    （2）从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究，再从抽取的8人中任取3人，求3人中含有醉酒驾车人数x的分布列和期望．

    查看答案和解析>>

    11、中国政府正式加入世贸组织后，从2000年开始，汽车进口关税将大幅度下降．若进口一辆汽车2001年售价为30万元，五年后（2006年）售价为y万元，每年下调率平均为x%，那么y和x的函数关系式为（　　）

    查看答案和解析>>

    中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量Q（简称血酒含量，单位是毫克/100毫升），当20≤Q＜80时，为酒后驾车；当Q≥80时，为醉酒驾车  哈尔滨市公安局交通管理部门于2010年3月的一天对某路段的一次拦查行动中，依法检查了200辆机动车驾驶员的血酒含量，其中查处酒后驾车的有6人，查处醉酒驾车的有4人，依据上述材料回答下列问题：
    （1）分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数；
    （2）从违法驾车的10人中抽取4人，求抽取到醉酒驾车人数ξ的分布列和期望；
    （3）饮酒后违法驾驶机动车极易发生交通事故，假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.2和0.5，且每位驾驶员是否发生交通事故是相互独立的  依此计算被查处的10名驾驶员中至少有一人发生交通事故的概率．

    查看答案和解析>>

    中国环保部部长在2012年“六•五”世界环境日高层论坛上表示，国家正在加大污水处理的投入，为此四川兰家沟污水处理站拟建一座平面图形为矩形且面积为2000m2的四级污水处理池，长，宽都不能超过60米，如果四周围池壁建造单价为400元/m，中间三道隔墙建造单价为300元/m，池底建造单价为100元/m2，池壁的厚度忽略不计．设污水池的长为x米，总造价为f（x）元．
    （1）求f（x）的解析式，并求出其定义域；
    （2）求f（x）的最小值，并求出此时污水池的长和宽．

    查看答案和解析>>

    一、ABCBD  BCABD

    二、11.2    12.     13.4    14.10    15. ①②③

    三、16. 解：（1），             3分

    由已知，得．         6分

    （2）由（1）得，      8分

    当时，的最小值为，             10分

    由，得值的集合为．   13分

    17. 解：（I）取AB的中点O，连接OP，OC      高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。PA=PB   高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。PO高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。AB

        又在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

          高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面ABC       4分

          又  PO高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面PAB，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面PAB高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。面ABC              6分

    （Ⅱ）以O为坐标原点， 分别以OB，OC，OP为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。轴，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。轴，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。轴建立坐标系，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。如图，则A高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   8分

     高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     设平面PAC的一个法向量为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。。

           高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

      令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     11分

    设直线PB与平面PAC所成角为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ，

    于是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。     13分

    18. 解：（1）；                4分

    （2）消费总额为1500元的概率是：                 5分

    消费总额为1400元的概率是：    6分

    消费总额为1300元的概率是：

    ＝，

    所以消费总额大于或等于1300元的概率是；              8分

    （3），

    ，

    ＝

    。所以的分布列为：

    0

    1

    2

    3

    0.294

    0.448

    0.222

    0.036

    数学期望是：。       13分

    19. 解：∵的右焦点 

    ∴椭圆的半焦距，又，

    ∴椭圆的， .椭圆方程为.

    （Ⅰ）当时，故椭圆方程为，      3分

    （Ⅱ）依题意设直线的方程为：，

    联立  得点的坐标为.      4分

    将代入得.

    设、，由韦达定理得，.   5分

    又，.

     

                    7分

    有实根， ∴点可以在圆上.        8分

    （Ⅲ）假设存在满足条件的实数，

    由解得：.     10分

    ∴，，又.即的边长分别是、、 .时，能使的边长是连续的自然数。      13分

    20. 解：（1）．                    1分

      　当时，，在上单调递增；                2分

    当，时，，在上单调递减；

    时，，在上单调递增．            3分

    综上所述，当时，的单调递增区间为；当时，的单调递增区间为，单调递减区间为．                     4分

    （2）充分性：时，由（1）知，在x=1处有极小值也是最小值，

    即。而在上单调递减，在上单调递增，

    所以在上有唯一的一个零点x=1．                    6分

    必要性：若函数f(x)存在唯一零点，即方程=0在上有唯一解，

    因, 由（1）知，在处有极小值也是最小值f(a)，

     f(a)=0,即．                        7分

    令， ．

    当时，，在上单调递增；当时，，

    在上单调递减。，=0只有唯一解．

    因此=0在上有唯一解时必有．

    综上：在时， =0在上有唯一解的充要条件是．    9分

    （3）证明：∵1<x<2, ∴.

     令，∴，11分

    由（1）知，当时，，∴，

    ∴．∴，                      12分

    ∴F（x）在（1，2）上单调递增，∴，

    ∴。∴．             14分

    21. （Ⅰ）解：考虑在矩阵作用下，求出变换后的三角形的顶点坐标，从而求得三角形的面积，可先求得，由＝，得点在矩阵作用下变换所得到的点，同理求得在矩阵作用下变换所得到的点分别是，，计算得△的面积为3．                7分

    （Ⅱ）解：直线的极坐标方程，则，

        即，所以直线的直角坐标方程为；     2分

    设，其中，则P到直线的距离

    ，其中，∴ 当时，的最大值为；当时，的最小值为。         7分

    （Ⅲ）解：由柯西不等式，得，    2分

    即．由条件，得．解得，  2分

    当且仅当 时等号成立．代入时，；时，．所以，的取值范围是．            7分

     

     


    同步练习册答案