
题目列表(包括答案和解析)
(14分)已知抛物线、椭圆、双曲线都经过点M(1,2),它们在x轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线方程;
(Ⅱ)若定点P(3,0),A为抛物线上任意一点,是否存在垂直于x轴的直线l被以AP为直径的圆截得的弦长为定值?若存在,求出l的方程;若不存在,说明理由。 (14分)
已知定义在 上的函数
上的函数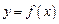 是偶函数,且
是偶函数,且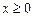 时,
时,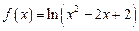 ,
,
(1)当 时,求
时,求 解析式;
解析式;
(2)写出 的单调递增区间。
的单调递增区间。
(14分)
函数 ,
,
(1)判断 的奇偶性;
的奇偶性;
(2)求证 在
在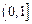 上是减函数。
上是减函数。
(14分)等差数列 中,前三项分别为
中,前三项分别为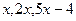 ,前
,前 项和为
项和为
(1)、求 和
和 ; (2)、求T=
; (2)、求T= 。
。
(14分) 已知等差数列的定义为:在一个数列中,从第二项起,如果每一项与它的前一项的差都为同一个常数,那么这个数列叫做等差数列,这个常数叫做该数列的公差.(1)类比等差数列的定义给出“等和数列”的定义;(2) 已知数列 是等和数列,且
是等和数列,且 ,公和为
,公和为 ,求
,求  的值,并猜出这个数列的通项公式(不要求证明)。
的值,并猜出这个数列的通项公式(不要求证明)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com