
题目列表(包括答案和解析)
(本题满分15分)
已知偶函数 满足:当
满足:当 时,
时,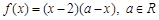 ,当
,当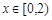 时,
时,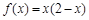
(1) 求当 时,
时,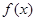 的表达式;
的表达式;
(2) 若直线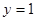 与函数
与函数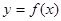 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数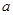 的取值范围。
的取值范围。
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
(本题满分15分)
已知偶函数 满足:当
满足:当 时,
时, ,当
,当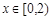 时,
时,
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 若直线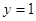 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
 本题满分15分)
本题满分15分) 数
数 满足:当
满足:当 时,
时, ,当
,当 时,
时,
 时,
时, 的表达式;
的表达式; 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 (3) 试讨论当实数
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。(本题满分15分)
把正整数按从小到大顺序排列成下列数表,数表中第 行共有
行共有 个正整数:
个正整数:

设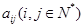 是位于数表中从上往下数第
是位于数表中从上往下数第 行、从左往右数第
行、从左往右数第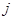 个数
个数
(1)若 ,求
,求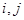 的值;
的值;
(2)记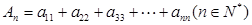 ,求数列
,求数列 的通项公式;
的通项公式;
(3)猜想 与
与 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(本题满分13分)本题共有2个小题,第1小题满分5分,第2小题满分8分.
某校15名学生组成该校“科技创新周”志愿服务队(简称“科服队”),他们参加活动的有关数据统计如下:
| 参加活动次数 | 1 | 2 | 3 |
| 人 数 | 3 | 4 | 8 |
(1)从“科服队”中任选3人,使得这3人参加活动次数各不相同,这样的选法共有多少种?
(2)从“科服队”中任选2人,求这2人参加活动次数之和大于3的概率.
说明
1. 本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.
2. 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅. 当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.
3. 第17题至第21题中右端所注分数,表示考生正确做到这一步应得的该题累加分数.
4. 给分或扣分均以1分为单位.
答案及评分标准
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ; 5.(理)
; 5.(理) 元;(文)0.7;
元;(文)0.7;
6.(理) ; (文)200赫兹; 7.(理)5; (文)p=4.
; (文)200赫兹; 7.(理)5; (文)p=4.
8.(理) ; (文)
; (文)
9. ; 10.(理)
; 10.(理) ; (文)方程为
; (文)方程为 .
.
11.(理) ; (文)
; (文) ; 12.12.
; 12.12.
13――16:A; C ; C; 理B文A
17.设熊猫居室的总面积为 平方米,由题意得:
平方米,由题意得: .… 6分
.… 6分
解法1: ,因为
,因为 ,而当
,而当 时,
时, 取得最大值75. 10分
取得最大值75. 10分
所以当熊猫居室的宽为
解法2: =75,当且仅当
=75,当且仅当 ,即
,即 时,
时, 取得最大值75.
…… 10分
取得最大值75.
…… 10分
所以当熊猫居室的宽为
18.理:如图,建立空间直角坐标系,可得有关点的坐标为 、
、 、
、 、
、 、
、 、
、 .
……2分
.
……2分
设平面 的法向量为
的法向量为 ,则
,则 ,
, .
.
因为 ,
, ,
……3分
,
……3分
 ,
, ,
,
所以 解得
解得 ,取
,取 ,得平面
,得平面 一个法向量
一个法向量 ,且
,且 .
……5分
.
……5分
(1)在平面 取一点
取一点 ,可得
,可得 ,于是顶点
,于是顶点 到平面
到平面 的距离
的距离 ,所以顶点
,所以顶点 到平面
到平面 的距离为
的距离为 ,
……8分
,
……8分
(2)因为平面 的一个法向量为
的一个法向量为 ,设
,设 与
与 的夹角为a,则
的夹角为a,则
 ,
……12分
,
……12分
结合图形可判断得二面角 是一个锐角,它的大小为
是一个锐角,它的大小为 .……14分
.……14分


文:(1)圆锥底面积为 cm2,
……1分
cm2,
……1分
设圆锥高为 cm,由体积
cm,由体积 ,
……5分
,
……5分
由 cm3得
cm3得 cm;
……8分
cm;
……8分
(2)母线长 cm,
……9分
cm,
……9分
设底面周长为 ,则该圆锥的侧面积=
,则该圆锥的侧面积= ,
……12分
,
……12分
所以该圆锥的侧面积= cm2.
……14分
cm2.
……14分
19.(理)(1) ;
……3分
;
……3分
(2)当 时,(
时,( )
)
 , ……6分
, ……6分
所以, (
( ).
……8分
).
……8分
(3)与(2)同理可求得: , ……10分
, ……10分
设 =
= ,
,
则 ,(用等比数列前n项和公式的推导方法)
,(用等比数列前n项和公式的推导方法) ,相减得
,相减得
 ,所以
,所以
 .
……14分
.
……14分
(文)(1)设数列前 项和为
项和为 ,则
,则 . ……3分
. ……3分
(2)公比 ,所以由无穷等比数列各项的和公式得:
,所以由无穷等比数列各项的和公式得:
数列 各项的和为
各项的和为 =1.
……7分
=1.
……7分
(3)设数列 的前
的前 项和为
项和为 ,当
,当 为奇数时,
为奇数时, =
=
 ;
……11分
;
……11分
当 为偶数时,
为偶数时, =
= . ……14分
. ……14分
即 .
……15分
.
……15分
20.(1) 即
即 ,又
,又 ,2分
,2分
所以 ,从而
,从而 的取值范围是
的取值范围是 . ……5分
. ……5分
(2) ,令
,令 ,则
,则 ,因为
,因为 ,所以
,所以 ,当且仅当
,当且仅当 时,等号成立,8分
时,等号成立,8分
由 解得
解得 ,所以当
,所以当 时,函数
时,函数 的最小值是
的最小值是 ;
……11分
;
……11分
下面求当 时,函数
时,函数 的最小值.
的最小值.
当 时,
时, ,函数
,函数 在
在 上为减函数.所以函数
上为减函数.所以函数 的最小值为
的最小值为 .
.
[当 时,函数
时,函数 在
在 上为减函数的证明:任取
上为减函数的证明:任取 ,
, ,因为
,因为 ,
, ,所以
,所以 ,
, ,由单调性的定义函数
,由单调性的定义函数 在
在 上为减函数.]
上为减函数.]
于是,当 时,函数
时,函数 的最小值是
的最小值是 ;当
;当 时,函数
时,函数 的最小值
的最小值 .
……15分
.
……15分
21.(1)由 解得
解得 ;由
;由 解得
解得 .
.
由点斜式写出两条直线 的方程,
的方程, ,
,
所以直线AB的斜率为 . ……4分
. ……4分
(2)推广的评分要求分三层
一层:点P到一般或斜率到一般,或抛物线到一般(3分,问题1分、解答2分)
例:1.已知 是抛物线
是抛物线 上的相异两点.设过点
上的相异两点.设过点 且斜率为-1的直线
且斜率为-1的直线 ,与过点
,与过点 且斜率为1的直线
且斜率为1的直线 相交于抛物线
相交于抛物线 上的一定点P
上的一定点P ,求直线AB的斜率;
,求直线AB的斜率;
2.已知 是抛物线
是抛物线 上的相异两点.设过点
上的相异两点.设过点 且斜率为-k 1的直线
且斜率为-k 1的直线 ,与过点
,与过点 且斜率为k的直线
且斜率为k的直线 相交于抛物线
相交于抛物线 上的一点P(4,4),求直线AB的斜率;
上的一点P(4,4),求直线AB的斜率;
3.已知 是抛物线
是抛物线 上的相异两点.设过点
上的相异两点.设过点 且斜率为-1的直线
且斜率为-1的直线 ,与过点
,与过点 且斜率为1的直线
且斜率为1的直线 相交于抛物线
相交于抛物线 上的一定点P
上的一定点P ,求直线AB的斜率; AB的斜率的值.
,求直线AB的斜率; AB的斜率的值.
二层:两个一般或推广到其它曲线(4分,问题与解答各占2分)
例:4.已知点R是抛物线 上的定点.过点P作斜率分别为
上的定点.过点P作斜率分别为 、
、 的两条直线
的两条直线 ,分别交抛物线于A、B两点,试计算直线AB的斜率.
,分别交抛物线于A、B两点,试计算直线AB的斜率.
三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法.)(7分,问题3分、解答4分)
例如:5.已知抛物线 上有一定点P,过点P作斜率分别为
上有一定点P,过点P作斜率分别为 、
、 的两条直线
的两条直线 ,分别交抛物线于A、B两点,试计算直线AB的斜率.
,分别交抛物线于A、B两点,试计算直线AB的斜率.
过点P( ),斜率互为相反数的直线可设为
),斜率互为相反数的直线可设为 ,
, ,其中
,其中 。
。
由 得
得 ,所以
,所以

同理,把上式中 换成
换成 得
得 ,所以
,所以
当P为原点时直线AB的斜率不存在,当P不为原点时直线AB的斜率为 。
。
(3)(理)点 ,设
,设 ,则
,则 .
.
设线段 的中点是
的中点是 ,斜率为
,斜率为 ,则
,则 =
= .12分
.12分
所以线段 的垂直平分线
的垂直平分线 的方程为
的方程为 ,
,
又点 在直线
在直线 上,所以
上,所以 ,而
,而 ,于是
,于是 .
……13分
.
……13分
(斜率
 ,则
,则 --------------------------------13分)
--------------------------------13分)
线段 所在直线的方程为
所在直线的方程为 ,
……14分
,
……14分
代入 ,整理得
,整理得 ……15分
……15分
 ,
, 。设
。设 线段长为
线段长为 ,则
,则
 =
=
 ……16分
……16分
因为 ,所以
,所以 ……18分
……18分
即: .(
.( )
)
(文)设 ,则
,则 .
……13分
.
……13分
设线段 的中点是
的中点是 ,斜率为
,斜率为 ,则
,则 =
= ,……15分
,……15分
线段 的垂直平分线
的垂直平分线 的方程为
的方程为 , ……17分
, ……17分
又点 在直线
在直线 上,所以
上,所以 ,
,
而 ,于是
,于是 .故线段AB中点的横坐标为
.故线段AB中点的横坐标为 . ……18分
. ……18分
&n
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com