
题目列表(包括答案和解析)
![]() ,故选C.
,故选C. ![]()
答案:C
【命题立意】:本题考查复数的除法运算,分子、分母需要同乘以分母的共轭复数,把分母变为实数,将除法转变为乘法进行运算.
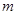 ,
,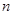 ,
,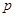 为常数,离心率为
为常数,离心率为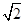 的双曲线
的双曲线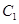 :
: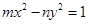 上的动点
上的动点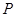 到两焦点的距离之和的最小值为
到两焦点的距离之和的最小值为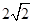 ,抛物线
,抛物线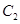 :
: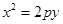
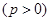 的焦点与双曲线
的焦点与双曲线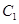 的一顶点重合。(Ⅰ)求抛物线
的一顶点重合。(Ⅰ)求抛物线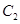 的方程;(Ⅱ)过直线
的方程;(Ⅱ)过直线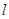 :
: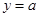 (
(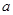 为负常数)上任意一点
为负常数)上任意一点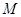 向抛物线
向抛物线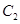 引两条切线,切点分别为
引两条切线,切点分别为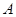 、
、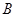 ,坐标原点
,坐标原点 恒在以
恒在以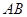 为直径的圆内,求实数
为直径的圆内,求实数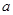 的取值范围。
的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为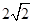 ,离心率为
,离心率为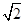 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为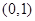 ,所以抛物线
,所以抛物线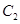 的方程
的方程
第二问中,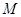 为
为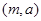 ,
,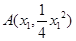 ,
, ,
,
故直线 的方程为
的方程为 ,即
,即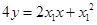 ,
,
所以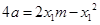 ,同理可得:
,同理可得: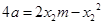
借助于根与系数的关系得到即 ,
,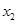 是方程
是方程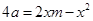 的两个不同的根,所以
的两个不同的根,所以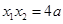
由已知易得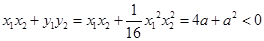 ,即
,即
解:(Ⅰ)由已知易得双曲线焦距为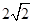 ,离心率为
,离心率为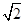 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为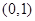 ,所以抛物线
,所以抛物线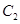 的方程
的方程
(Ⅱ)设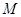 为
为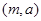 ,
,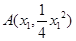 ,
, ,
,
故直线 的方程为
的方程为 ,即
,即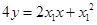 ,
,
所以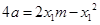 ,同理可得:
,同理可得: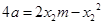 ,
,
即 ,
,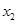 是方程
是方程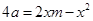 的两个不同的根,所以
的两个不同的根,所以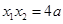
由已知易得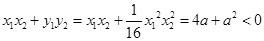 ,即
,即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 证人所说的颜色(正确率80%) | |||
| 真实颜色 | 绿色(辆) | 红色(辆) | 合计 |
| 绿色(85%) | 1700 | ||
| 红色(15%) | 300 | ||
| 合计(辆) | 2000 | ||
 如图,A处建有一个补给站,在A正西120海里处有一个港口B,一艘科考船从B出发,沿北偏东30°的方向,以20海里/小时的速度驶离港口.同时一艘为科考船运送补给的快艇从A出发,沿北偏西30°的方向,以60海里/小时的速度行驶,1小时后补给船行驶至C处,发生故障停留了1小时.快艇为在最短时间内将补给送到科考船,在C处调整航向后继续以60海里/小时的速度直线行驶,恰好与科考船在D处相遇,求相遇时科考船共行驶了多少小时.
如图,A处建有一个补给站,在A正西120海里处有一个港口B,一艘科考船从B出发,沿北偏东30°的方向,以20海里/小时的速度驶离港口.同时一艘为科考船运送补给的快艇从A出发,沿北偏西30°的方向,以60海里/小时的速度行驶,1小时后补给船行驶至C处,发生故障停留了1小时.快艇为在最短时间内将补给送到科考船,在C处调整航向后继续以60海里/小时的速度直线行驶,恰好与科考船在D处相遇,求相遇时科考船共行驶了多少小时.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com