
题目列表(包括答案和解析)
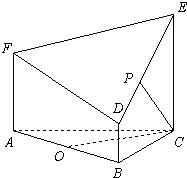 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点. 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得,已知FA⊥平面ABC,AB=2,BD=1,AF=2, CE=3,O为AB的中点.

(1)求证:OC⊥DF;
(2)求平面DEF与平面ABC相交所成锐二面角的大小;
(3)求多面体ABC—FDE的体积V.
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得,已知FA⊥平面ABC,AB=2,BD=1,AF=2, CE=3,O为AB的中点.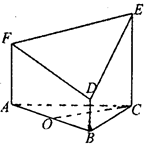
(1)求证:OC⊥DF;
(2)求平面DEF与平面ABC相交所成锐二面角的大小;
(3)求多面体ABC—FDE的体积V.
 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥1.C 2.C 3.B 4.A 5.C 6.C 7.D 8.C 9.D 10.B
1l.B 12.A
2.解析:文科数学.files/image250.gif)
文科数学.files/image252.gif)
文科数学.files/image254.gif) ,∴选C.
,∴选C.
3.解析:文科数学.files/image256.gif) 是增函数
是增函数 文科数学.files/image258.gif)
故文科数学.files/image260.gif) ,即
,即文科数学.files/image262.gif)
又文科数学.files/image264.gif)
文科数学.files/image266.gif) ,故选B.
,故选B.
4.解析:如图作出可行域,作直线文科数学.files/image268.gif) ,平移直线
,平移直线文科数学.files/image270.gif) 至
至文科数学.files/image272.gif) 位置,使其经过点
位置,使其经过点文科数学.files/image106.gif) .此时目标函数取得最大值(注意
.此时目标函数取得最大值(注意文科数学.files/image028.gif) 与
与文科数学.files/image276.gif) 反号)
反号)
由文科数学.files/image278.gif) 得
得文科数学.files/image280.gif)
文科数学.files/image282.jpg)
文科数学.files/image284.gif) ,故选A
,故选A
5.解析:设有人投中为事件文科数学.files/image106.gif) ,则
,则文科数学.files/image287.gif) ,
,文科数学.files/image289.gif)
故选C.
6.解析:文科数学.files/image036.gif) 展开式中通项;
展开式中通项;
文科数学.files/image292.gif)
由文科数学.files/image294.gif) ,得
,得文科数学.files/image296.gif) ,故选C.
,故选C.
7.解析:文科数学.files/image298.gif)
由文科数学.files/image300.gif) 得
得文科数学.files/image302.gif)
文科数学.files/image304.gif) ,故选D.
,故选D.
8.略
9.解析:由文科数学.files/image306.gif) 得准线方程
得准线方程文科数学.files/image308.gif) ,双曲线准线方程为
,双曲线准线方程为文科数学.files/image310.gif)
文科数学.files/image312.gif) ,解得
,解得文科数学.files/image314.gif) ,
,
文科数学.files/image316.gif) ,故选D.
,故选D.
10.解析:设正四面体的棱长为2,取文科数学.files/image318.gif) 中点为
中点为文科数学.files/image320.gif) ,连接
,连接文科数学.files/image322.gif) ,则
,则文科数学.files/image324.gif) 为
为文科数学.files/image079.gif) 与
与文科数学.files/image081.gif) 所成的角,在
所成的角,在文科数学.files/image328.gif) 中
中
文科数学.files/image330.jpg)
文科数学.files/image332.gif)
文科数学.files/image334.gif) ,故选B.
,故选B.
11.解析:
文科数学.files/image336.jpg)
由题意文科数学.files/image338.gif) ,则
,则文科数学.files/image340.gif) ,故选B.
,故选B.
12.解析:由已知文科数学.files/image342.gif) ,
,
文科数学.files/image344.gif) 为球的直么
为球的直么
文科数学.files/image346.gif) ,又
,又文科数学.files/image348.gif) ,
,
设文科数学.files/image350.gif) ,则
,则文科数学.files/image352.gif)
文科数学.files/image354.gif) ,
,
文科数学.files/image356.gif)
又由文科数学.files/image358.gif) ,解得
,解得文科数学.files/image360.gif)
文科数学.files/image362.gif) ,故选A.
,故选A.
另法:将四面体文科数学.files/image102.gif) 置于正方休中.
置于正方休中.
正方体的对角线长为球的直径,由此得文科数学.files/image365.gif) ,然后可得
,然后可得文科数学.files/image367.gif) .
.
二、填空题
13.3;解析:文科数学.files/image369.gif) 在
在文科数学.files/image014.gif) 上的投影是
上的投影是文科数学.files/image372.gif) .
.
14.(0.2);解析:由文科数学.files/image374.gif) ,解得
,解得文科数学.files/image376.gif) .
.
15.文科数学.files/image378.gif)
解析:文科数学.files/image380.gif) ,
,
文科数学.files/image382.gif)
由余弦定理文科数学.files/image384.gif) 为钝角
为钝角
文科数学.files/image386.gif) ,即
,即文科数学.files/image388.gif) ,
,
解得文科数学.files/image378.gif) .
.
16.②③;
文科数学.files/image391.jpg)
解析:容易知命题①是错的,命题②、③都是对的,对于命题④我们考查如图所示的正方体,政棱长为文科数学.files/image155.gif) ,显然
,显然文科数学.files/image394.gif) 与
与文科数学.files/image396.gif) 为平面
为平面文科数学.files/image398.gif) 内两条距离为
内两条距离为文科数学.files/image155.gif) 的平行直线,它们在底面
的平行直线,它们在底面文科数学.files/image102.gif) 内的射影
内的射影文科数学.files/image077.gif) 、
、文科数学.files/image403.gif) 仍为两条距离为
仍为两条距离为文科数学.files/image155.gif) 的平行直线.但两平面
的平行直线.但两平面文科数学.files/image398.gif) 与
与文科数学.files/image102.gif) 却是相交的.
却是相交的.
三、
17.解:(1)文科数学.files/image408.gif) ,
,
文科数学.files/image410.gif) ,
,
即文科数学.files/image412.gif) ,故
,故文科数学.files/image414.gif) .
.
(2)文科数学.files/image416.gif)
由文科数学.files/image418.gif) 得
得文科数学.files/image420.gif) .
.
设文科数学.files/image014.gif) 边上的高为
边上的高为文科数学.files/image423.gif) 。则
。则文科数学.files/image425.gif)
文科数学.files/image427.gif) .
.
18.(1)设甲、乙两人同时参加文科数学.files/image106.gif) 灾区服务为事件
灾区服务为事件文科数学.files/image106.gif) ,则
,则文科数学.files/image431.gif) .
.
(2)记甲、乙两人同时参加同一灾区服务为事件文科数学.files/image164.gif) ,那么
,那么文科数学.files/image434.gif) .
.
19.解:
文科数学.files/image436.jpg)
(1)文科数学.files/image438.gif) 平面
平面文科数学.files/image440.gif)
∵二面角文科数学.files/image182.gif) 为直二面角,且
为直二面角,且文科数学.files/image443.gif) ,
,
文科数学.files/image445.gif) 平面
平面文科数学.files/image447.gif)
文科数学.files/image449.gif) 平面
平面文科数学.files/image193.gif) .
.
(2)(法一)连接文科数学.files/image452.gif) 交
交文科数学.files/image318.gif) 交于
交于文科数学.files/image455.gif) 点,连接
点,连接文科数学.files/image457.gif) 是边长为2的正方形,
是边长为2的正方形, 文科数学.files/image459.gif) ,
,
文科数学.files/image461.gif)
文科数学.files/image463.gif) 平面
平面文科数学.files/image189.gif) ,由三垂线定理逆定理得
,由三垂线定理逆定理得文科数学.files/image466.gif)
文科数学.files/image468.gif) 是二面角
是二面角文科数学.files/image195.gif) 的平面角
的平面角
由(1)文科数学.files/image191.gif) 平面
平面文科数学.files/image472.gif) ,
,
文科数学.files/image474.gif) .
.
在文科数学.files/image476.gif) 中,
中,文科数学.files/image478.gif)
∴在文科数学.files/image480.gif) 中,
中,文科数学.files/image482.gif)
故二面角文科数学.files/image195.gif) 等于
等于文科数学.files/image485.gif) .
.
(2)(法二)利用向量法,如图以文科数学.files/image077.gif) 之中点
之中点文科数学.files/image488.gif) 为坐标原点建立空间坐标系
为坐标原点建立空间坐标系文科数学.files/image490.gif) ,则
,则
文科数学.files/image492.jpg)
文科数学.files/image494.gif)
文科数学.files/image496.gif) ,
,
设平面文科数学.files/image189.gif) 的法向量分别为
的法向量分别为文科数学.files/image499.gif) ,则由
,则由
文科数学.files/image501.gif) 得
得文科数学.files/image503.gif) ,而平面
,而平面文科数学.files/image505.gif) 的一个法向理
的一个法向理文科数学.files/image507.gif)
文科数学.files/image509.gif)
故所求二面角等于文科数学.files/image511.gif) .
.
20.解:(1)由题设文科数学.files/image513.gif) ,即
,即文科数学.files/image515.gif)
易知文科数学.files/image517.gif) 是首项为
是首项为文科数学.files/image519.gif) ,公差为2的等差数列,
,公差为2的等差数列,
∴通项公式为文科数学.files/image521.gif) ,
,
(2)由题设,文科数学.files/image523.gif) ,得
,得文科数学.files/image525.gif) 是以
是以文科数学.files/image527.gif) 公比为
公比为文科数学.files/image529.gif) 的等比数列.
的等比数列.
文科数学.files/image531.gif)
由文科数学.files/image533.gif) 得
得文科数学.files/image535.gif) .
.
21.解:(1)由题意文科数学.files/image537.gif) ,由抛物线定义可求得曲线
,由抛物线定义可求得曲线文科数学.files/image166.gif) 的方程为
的方程为文科数学.files/image540.gif) .
.
(2)证明:设点文科数学.files/image106.gif) 、
、文科数学.files/image164.gif) 的坐标分别为
的坐标分别为文科数学.files/image544.gif)
若文科数学.files/image077.gif) 直线有斜率时,其坐标满足下列方程组:
直线有斜率时,其坐标满足下列方程组:
文科数学.files/image547.gif) ,
, 文科数学.files/image549.gif)
若文科数学.files/image077.gif) 没有斜率时,
没有斜率时,文科数学.files/image077.gif) 方程为
方程为文科数学.files/image553.gif) .
.
又文科数学.files/image555.gif) .
.
文科数学.files/image557.gif)
文科数学.files/image559.gif) ;又
;又文科数学.files/image561.gif) ,
,
文科数学.files/image563.gif)
文科数学.files/image565.gif) .
.
22.(1)解:方程文科数学.files/image241.gif) 可化为
可化为文科数学.files/image568.gif) .
.
当文科数学.files/image570.gif) 时,
时,文科数学.files/image572.gif) ,又
,又文科数学.files/image574.gif) ,于是
,于是文科数学.files/image576.gif) ,解得
,解得文科数学.files/image578.gif) ,故
,故文科数学.files/image580.gif) .
.
(2)解:设文科数学.files/image582.gif) 为曲线上任一点,由
为曲线上任一点,由文科数学.files/image584.gif) 知曲线在点
知曲线在点文科数学.files/image582.gif) 处的切线方程为
处的切线方程为文科数学.files/image586.gif) ,即
,即文科数学.files/image588.gif) .
.
令文科数学.files/image246.gif) ,得
,得文科数学.files/image591.gif) ,从而得切线与直线
,从而得切线与直线文科数学.files/image246.gif) 的交点坐标为
的交点坐标为文科数学.files/image594.gif)
令文科数学.files/image596.gif) ,得
,得文科数学.files/image598.gif) ,从而得切线与直线
,从而得切线与直线文科数学.files/image248.gif) 的交点坐标为
的交点坐标为文科数学.files/image601.gif) .所以点
.所以点文科数学.files/image582.gif) 处的切线与直线
处的切线与直线文科数学.files/image604.gif) 所围成的三角形面积为
所围成的三角形面积为文科数学.files/image606.gif) .故曲线
.故曲线文科数学.files/image237.gif) 上任一点处的切线与直线
上任一点处的切线与直线文科数学.files/image604.gif) 所围成的三角形的面积为定值,此定值为6.
所围成的三角形的面积为定值,此定值为6.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com