题目列表(包括答案和解析)
甲、乙两袋装有大小相同的红球和白球，其中甲袋装有1个红球，4个白球；乙袋装有2个红球，3个白球。现从甲、乙两袋中各任取2个小球。
（1）用
表示取到的4个球中红球的个数，求的分布列及的数学期望；
（2）求取到的4个球中至少2个红球的概率。
甲、乙两袋装有大小相同的红球和白球，其中甲袋装有1个红球，4个白球；乙袋装有2个红球，3个白球。现从甲、乙两袋中各任取2个球。
（Ⅰ）用
表示取到的4个球中红球的个数，求的分布列及的数学期望；
（Ⅱ）求取到的4个球中至少有2个红球的概率．
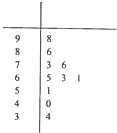（2012•茂名二模）某校高一级数学必修I模块考试的成绩分为四个等级，85分-100分为A等，70分-84分为B等，55分-69分为C等，54分以下为D等．右边的茎叶图（十位为茎，个位为叶）记录了某班某小组10名学生的数学必修I模块考试成绩．一个袋中装有10个红球，20个白球，这些球除颜色外完全相同，一次从中摸出5个球，随机变量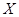
表示取到的红球数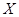，服从超几何分布
，则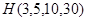
=
（用组合数作答）
一：选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
B
B
B
B
D
B
D
C
C
A
二、填空题：
13、0
14、
15、 
16、①②
三、解答题：
17、（Ⅰ）∵
∴
的最大值为
，最小正周期是
。…………………6分
注：得出表达式的简化形式得4分，最大值、周期各得1分。
（Ⅱ）由（Ⅰ）知
即
成立的
的取值集合是
………10分
注：正确写出正弦的单调增区间2分，答案正确2分。
18、解：（Ⅰ）
， 
， 
随机变量
的分布列为
0
1
2
3
P
数学期望
………………………………………8分
注：每个概率算对得1分，分布列2分，期望2分。
(II)所求的概率
…………12分
注：知道概率加法公式得2分，结果正确得2分。
19、(本题满分12分)
证明：（1）在直三棱柱
，
∵底面三边长
，
，
∴ 
，
--------------------------------1分
又直三棱柱
中 
，
且
∴
---------------------------------3分
而
∴
；
---------------------------------4分
（2）设
与
的交点为
，连结
，---------------------5分
∵D是AB的中点，E是BC1的中点，
∴ 
，
----------------------------7分
∵ 
，
，
∴
.
----------------------------8分
（3）过点C作CF⊥AB于F，连接C
由已知C1C垂直平面ABC，则∠C1FC为二面角
的平面角 ----------9分
在Rt△ABC中，
，
,
,则
----------10分
又
∴ 
----------11分
∴二面角的正切值为
---------- 12分
（另：可以建立空间直角坐标系用向量方法完成，酌情给分，过程略）
20、解（1）
∵
在
增函数，（0，2）为减函数
………………………………………………2分
（2）
， …………………
4分
5分
……………………7分
（3）
，
……………………………………………………………………12分
21、 解：(1)f(x)对任意
2分
令
4分
（2）解：数列{an}是等差数列 f(x)对任意x∈R都有
则令
5分
∴{an}是等差数列
8分
（3）解：由（2）有
9分
∴Tn≤Sn 该题也可用数学归纳法做。 12分
22、解：(1)∵
∴线段NP是AM的垂直平分线， 2分
∴
3分
∵
∴点N的轨迹是以点C、A为焦点的椭圆； 4分
∴点N的轨迹E的方程是
5分
（2）当直线的斜率不存在时，
，
，∴
=
；
6分
当直线的斜率存在时，设其方程为
,
,△
,
7分
设G(x1,y1),H(x2,y2)
,
,∵
,∴
8分
,
,
9分
,
,
,
10分
，
∵点
在点
、
之间 ， ∴<1
11分
∴的取值范围是[
）。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com