练习册

  • 练习册
  • 试题
    (II)若射线与椭圆的交点为过作倾斜角互补的两条直线.分别与椭圆交于两点(异于).求证: 直线的斜率定值, 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

            椭圆的右焦点为F，过原点和x轴不重合的直线与椭圆E交于A，B，两点，|AF|+|BF|=4，的最小值为0.5。

       （I）求椭圆E的方程；

       （II）若直线与椭圆E交于M，N两点（其中），以线段MN为直径的圆过E的右顶点，求证：直线过定点。

    查看答案和解析>>

    （08年芜湖一中）已知在平面直角坐标系中，若在曲线的方程中以为正实数）代替得到曲线的方程，则称曲线关于原点“伸缩”，变换称为“伸缩变换”，称为伸缩比．

    (1)已知曲线的方程为，伸缩比，求关于原点“伸缩变换”后所得曲线的标准方程；

    (2)射线的方程，如果椭圆经“伸缩变换”后得到椭圆，若射线与椭圆分别交于两点，且，求椭圆的标准方程；

    (3)对抛物线，作变换，得抛物线；对作变换得抛物线，如此进行下去，对抛物线作变换,得抛物线．若，求数列的通项公式．

    查看答案和解析>>

    （2013•黑龙江二模）已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）经过A（2，0）和B（1，
    3
    2
    ）两点，O为坐标原点．
    （I ）求椭圆C的方程；
    （II）若以点O为端点的两条射线与椭圆c分别相交于点M，N且
    MN
    丄
    ON
    ，证明：点O到直线MN的距离为定值．

    查看答案和解析>>

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）经过A（2，0）和B（1，
    3
    2
    ）两点，O为坐标原点．
    （I ）求椭圆C的方程；
    （II）若以点O为端点的两条射线与椭圆c分别相交于点M，N且
    MN
    丄
    ON
    ，证明：点O到直线MN的距离为定值．

    查看答案和解析>>

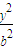    已知椭圆C：+=1（a＞b＞0）经过A（2，0）和B（1，）两点，O为坐标原点．
    （I ）求椭圆C的方程；
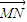    （II）若以点O为端点的两条射线与椭圆c分别相交于点M，N且丄，证明：点O到直线MN的距离为定值．

    查看答案和解析>>

    一、选择题：

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    B

    D

    A

    C

    D

    C

    C

    A

    D

    B

    D

    C

    二、填空题（本大题共4小题，每小题4分，共16分）

    13、；   14、；   15、32；     16、2

    三、解答题：（本大题共6小题，共74分，）

    17、解：（I）

                    

                     ……………………………………………………4分

        ………………………………………………………………6分

       （II）由余弦定理得

       

        ……………………………………………………………………9分

        而，

        函数

        当………………………………………12分

    18、解：由上表可求出10次记录下的有记号的红鲫鱼与中国金鱼数目的平均数均为20，故可认为池塘中的红鲫鱼与中国金鱼的数目相同，设池塘中两种鱼的总数是，则有

    ，   即   ，        ------------4分

                        

    所以，可估计水库中的红鲫鱼与中国金鱼的数量均为25000．    ------------6分

    （Ⅱ）显然，，                                 -----------9分

    其分布列为

    0

    1

    2

    3

    4

    5

    ---------11分

    数学期望．                                  -----------12分

    ∵DE⊥EB，∴四边形CDEF是矩形，

    ∵CD=1，∴EF=1。

    ∵四边形ABCD是等腰梯形，AB=3。

    ∴AE=BF=1。

    ∵∠BAD=45°，∴DE=CF=1。

    连结CE，则CE=CB=

    ∵EB=2，∴∠BCE=90°。

    则BC⊥CE。                                                 …………3分

    在图2中，∵AE⊥EB，AE⊥ED，EB∩ED=E，

    ∴AE⊥平面BCDE。

    ∵BC平面BCDE，∴AE⊥BC。                                 …………4分

    ∵AE∩CE=E，∴BC⊥平面AEC。                                …………5分

       （II）∵AE⊥平面BCDE，CF平面BCDE。

    ∴AE⊥CF。

    ∴CF⊥平面ABE。

    过C作CG⊥AB，连结FG，则∠CGF就是二面角C―AB―E的平面角。……6分

    又CF=1，AE=1，CE=BC=。

    ∴AC=

    在Rt△ACB中，AB=

    又AC?BC=AB?CG，∴CG=     ∴FG=   

    ∴二面角C―AB―E的正切值为                             …………8分

       （III）用反证法。

    假设EM∥平面ACD。                                         

    ∵EB∥CD，CD平面ACD，EB平面ACD，

    ∴EB∥平面ACD。∵EB∩EM=E，∴面AEB∥面ACD                  …………10分

    而A∈平面AEB，A∈平面ACD，

    与平面AEB//平面ACD矛盾。

    ∵假设不成立。

        ∴EM与平面ACD不平行。………………………………12分

    20、（I）解：由得，

     ，，

    ∴，  

    ∵为等比数列   ∴∴=                             3分                                                 

    （II）证明：因为方程的两根为3、7，

    由题意知， 即，∴

    ∴等差数列的公差，∴

    ∴                        6分

    要证，只要证明， 即

    下面用数学归纳法证明成立

    （i）当，2，3时，不等式显然成立，

    （ii）假设当（）时，不等式成立，即

    当+1时，

    即，此时不等式也成立．

    由（i）（ii）知，对任意，成立．

    所以，对任意，．                              9分

    （III）证明：由（II）已证成立，两边取以3为底的对数得，

    ∴

    ∴，  ∴ w.w.w.k.s.5 u.c.o.m             12分

    21、解：（I）设椭圆方程为，         1分

    则由题意有，，                       2分

    因此，，                        3分

    所以椭圆的方程为。                          4分

    （II）∵　斜率存在，不妨设，求出．   5分

    直线 方程为，直线 方程  …………6分

    　　分别与椭圆方程联立，可解出，   7分

    ∴　．∴　为定值．       8分

    （Ⅲ）设直线AB方程为，与联立，消去得

    ．                                  9分

    由 >0得-4＜ ＜4，且 ≠0，点 到 的距离为．………… 10分

                   11分

    　   设△的面积为S．　∴　．

    当时，得．                       12分

    22、（I）解：当

    此时， 的极小值为，无极大值                        …………4分

    （II）解：

               …………8分

    （III）由（I）知：上为增函数，

     

     


    同步练习册答案