
题目列表(包括答案和解析)
(09 年石景山区统一测试文)(14分)
已知函数![]() ,
,![]() ,若
,若![]() ,且
,且![]() 的图象
的图象
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(09 年石景山区统一测试文)(14分)
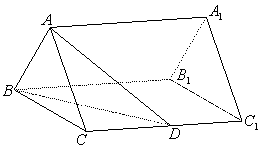
如图,已知正三棱柱![]() ―
―![]() 的底面边长是
的底面边长是![]() ,侧棱
,侧棱![]() 的长是
的长是![]() ,点
,点![]() 是
是
侧棱![]() 的中点.
的中点.
(Ⅰ)求直线![]() 与侧面
与侧面![]() 所成的角;
所成的角;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
(09 年石景山区统一测试文)(12分)
一项体育比赛按两轮排定名次,每轮由![]() 两种难度系数的
两种难度系数的![]() 个动作构成.某选手参赛
个动作构成.某选手参赛
方案如下表所示:
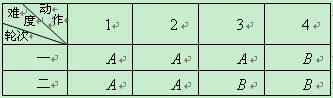
若这个选手一次正确完成难度系数为![]() 的动作的概率为
的动作的概率为![]() ,一次正确完成难度系数为
,一次正确完成难度系数为
![]() 的动作的概率为
的动作的概率为![]() .
.
(Ⅰ) 求这个选手在第一轮中前![]() 个动作都正确完成的概率;
个动作都正确完成的概率;
(Ⅱ) 求这个选手在第一轮中恰有![]() 个动作正确完成的概率;
个动作正确完成的概率;
(09 年石景山区统一测试文)(13分)
已知向量![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(09 年石景山区统一测试理)(13分)
已知![]() 为函数
为函数![]() 图象上一点,
图象上一点,![]() 为坐标原点.记直线
为坐标原点.记直线![]() 的斜率
的斜率![]() .
.
(Ⅰ)同学甲发现:点![]() 从左向右运动时,
从左向右运动时,![]() 不断增大,试问:他的判断是否正确?
不断增大,试问:他的判断是否正确?
若正确,请说明理由;若不正确,请给出你的判断;
(Ⅱ)求证:当![]() 时,
时, ;
;
(Ⅲ)同学乙发现:总存在正实数![]() 、
、![]()
![]() ,使
,使![]() .试问:他的判断是否正
.试问:他的判断是否正
一、选择题:
1.D 2.A 3.B 4.B 5.A 6.C 7.D 8.C 9.B 10.B 11.C 12.B
|