
题目列表(包括答案和解析)
A、
| ||
B、
| ||
C、
| ||
D、
|
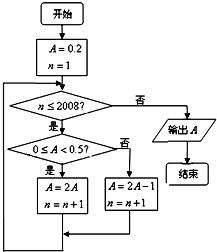
 13、已知某程序框图如图所示,则该程序运行后输出的结果为
13、已知某程序框图如图所示,则该程序运行后输出的结果为 已知某程序框图如图所示,则该程序运行后输出的结果为
已知某程序框图如图所示,则该程序运行后输出的结果为已知某程序框图如图所示,则该程序运行后,输出的结果为( )

A.0.6 B.0.8
C.0.5 D.0.2
已知某程序框图如图所示,则该程序运行后输出的结果为( )

A. B.
B.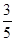 C.
C.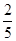 D.
D.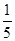
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. A 2. B 3. C 4. A 5.B
6. D 7. A 8. C 9. D 10.C
二、填空题:本大题共4小题,每小题4分,共16分.
11.  12.
12. 13.24
14.
13.24
14.
15.168 16.①②③ 17.1:(-6):5:(-8)
三、解答题:本大题共6小题,共74分.
18.解:(Ⅰ)由

 ---------4分
---------4分
由 ,得
,得
即
则 ,即
,即 为钝角,故
为钝角,故 为锐角,且
为锐角,且
则
故 . ---------8分
. ---------8分
(Ⅱ)设 ,
,
由余弦定理得
解得
故 .
---------14分
.
---------14分
19.解:(1) --------4分
--------4分
(2)x可能取的所有值有2,3,4 --------5分


 --------8分
--------8分
∴x的分布列为:








∴Ex= --------10分
--------10分
(3)当 时,取出的3张卡片上的数字为1,2,2或1,2,3
时,取出的3张卡片上的数字为1,2,2或1,2,3
当取出的卡片上的数字为1,2,2或1,2,3的概率为 ,
,
∴ --------14分
--------14分
 20.解:(Ⅰ)EF⊥DN,EF⊥BN,
20.解:(Ⅰ)EF⊥DN,EF⊥BN,
∴EF⊥平面BDN,
∴平面BDN⊥平面BCEF,
又因为BN为平面BDN与平面BCEF的交线,
∴D在平面BCEF上的射影在直线BN上
而D在平面BCEF上的射影在BC上,
∴D在平面BCEF上的射影即为点B,即BD⊥平面BCEF. --------4分
(Ⅱ)法一.如图,建立空间直角坐标系,
∵在原图中AB=6,∠DAB=60°,
则BN= ,DN=
,DN= ,∴折后图中BD=3,BC=3
,∴折后图中BD=3,BC=3
∴ ,
,

∴

∴
∴折后直线DN与直线BF所成角的余弦值为 . --------9分
. --------9分
法二.在线段BC上取点M,使BM=FN,则MN//BF
∴∠DNM或其补角为DN与BF所成角。
又MN=BF=2, DM= ,
, 。
。
∴
∴折后直线DN与直线BF所成角的余弦值为 。
。
(Ⅲ)∵AD//EF,
∴A到平面BNF的距离等于D到平面BNF的距离,
∴
即所求三棱锥的体积为 . --------14分
. --------14分
21.解:(Ⅰ)(?)由已知可得 ,
,
则所求椭圆方程 . --------3分
. --------3分
(?)由已知可得动圆圆心轨迹为抛物线,且抛物线 的焦点为
的焦点为 ,准线方程为
,准线方程为 ,则动圆圆心轨迹方程为
,则动圆圆心轨迹方程为 . --------6分
. --------6分
(Ⅱ)当直线MN的斜率不存在时,|MN|=4,
此时PQ的长即为椭圆长轴长,|PQ|=4,
从而 .
--------8分
.
--------8分
设直线 的斜率为
的斜率为 ,则
,则 ,直线
,直线 的方程为:
的方程为:
直线PQ的方程为 ,
,
设
由 ,消去
,消去 可得
可得
由抛物线定义可知:
 ----10分
----10分
由 ,消去
,消去 得
得 ,
,
从而 ,
--------12分
,
--------12分
∴
令 ,
,
∵k>0,则
则

所以 --------14分
--------14分
所以四边形 面积的最小值为8.
--------15分
面积的最小值为8.
--------15分
22.解:(Ⅰ)

∵ 为
为 的极值点,∴
的极值点,∴
∴ 且
且
∴ .
.
又当 时,
时, ,从而
,从而 为
为 的极值点成立。
的极值点成立。
--------4分
(Ⅱ)因为 在
在 上为增函数,
上为增函数,
所以 在
在 上恒成立. --------6分
上恒成立. --------6分
若 ,则
,则 ,
,
∴ 在
在 上为增函数不成立;
上为增函数不成立;
若 ,由
,由 对
对 恒成立知
恒成立知 。
。
所以 对
对 上恒成立。
上恒成立。
令 ,其对称轴为
,其对称轴为 ,
,
因为 ,所以
,所以 ,从而
,从而 在
在 上为增函数。
上为增函数。
所以只要 即可,即
即可,即
所以
又因为 ,所以
,所以 .
--------10分
.
--------10分
(Ⅲ)若 时,方程
时,方程
可得
即 在
在 上有解
上有解
即求函数 的值域.
的值域.
法一:
令
由
∵
∴当 时,
时, ,从而
,从而 在(0,1)上为增函数;
在(0,1)上为增函数;
当 时,
时, ,从而
,从而 在(1,+∞)上为减函数。
在(1,+∞)上为减函数。
∴ ,而
,而 可以无穷小。
可以无穷小。
∴ 的取值范围为
的取值范围为 .
--------15分
.
--------15分
法二:

当 时,
时, ,所以
,所以 在
在 上递增;
上递增;
当 时,
时, ,所以
,所以 在
在 上递减;
上递减;
又 ,∴令
,∴令 ,
, .
.
∴当 时,
时, ,所以
,所以 在
在 上递减;
上递减;
当 时,
时, ,所以
,所以 在
在 上递增;
上递增;
当 时,
时, ,所以
,所以 在
在 上递减;
上递减;
又当 时,
时, ,
,

当 时,
时,  ,则
,则 ,且
,且
所以 的取值范围为
的取值范围为 . --------15
. --------15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com