(1)地球绕太阳公转的周期为T
1,轨道半径为R
1,月球绕地球公转的周期为T
2,轨道半径为R
2,则太阳的质量是地球质量的
倍.
(2)将一单摆装置竖直悬挂于某一深度为h(未知)且开口向下的小筒中(单摆的下部分露于筒外),如图(甲)所示,将悬线拉离平衡位置一个小角度后由静止释放,设单摆振动过程中悬线不会碰到筒壁,如果本实验的长度测量工具只能测量出筒的下端口到摆球球心间的距离l,并通过改变l而测出对应的摆动周期T,再以T
2为纵轴、l为横轴做出函数关系图象,就可以通过此图象得出小简的深度h和当地的重力加速度g.

①现有如下测量工具:A.时钟;B.秒表; C.天平;D.毫米刻度尺.
本实验所需的测量工具有
BD
BD
;
②如果实验中所得到的T
2-l,关系图象如图(乙)所示,那么真正的图象应该是a,b,c中的
a
a
;
③由图象可知,小筒的深度h=
0.3
0.3
m;当地g=
9.86
9.86
m/s
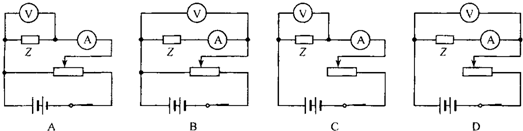
2(3)影响物质材料电阻率的因素很多,一般金属材料的电阻率随温度的升高而增大,而半导体材料的电阻率则与之相反,随温度的升高而减少.某课题研究组需要研究某种导电材料的导电规律,他们用该种导电材料制作成电阻较小的线状元件Z做实验,测量元件Z中的电流随两端电压从零逐渐增大过程中的变化规律.
①他们应选用下图所示的哪个电路进行实验?答:
A
A
②实验测得元件z的电压与电流的关系如下表所示.根据表中数据,判断元件Z是金属材料还是半导体材料?答:
半导体
半导体
.
| U(V) |
0 |
0.40 |
0.60 |
0.80 |
1.00 |
1.20 |
1.50 |
1.60 |
| I(A) |
0 |
0.20 |
0.45 |
0.80 |
1.25 |
1.80 |
2.81 |
3.20 |
③把元件Z接入如图丙所示的电路中,当电阻R的阻值为R
1=2Ω时,电流表的读数为1.25A;当电阻R的阻值为R
2=3.6Ω时,电流表的读数为0.80A.结合上表数据,求出电源的电动势为
4.0
4.0
V,内阻为
0.40
0.40
Ω.(不计电流表的内阻,结果保留两位有效数字)
④用螺旋测微器测得线状元件Z的直径如图丁所示,则元件Z的直径是
1.990
1.990
mm.


