
题目列表(包括答案和解析)
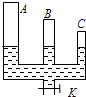 如图所示,上端封闭的连通器A、B、C 三管中水银面相平,三管横截面积关系为SA>SB>SC,管内水银面上方的空气柱长度为hA>hB>hC,若从下方通过阀门K流出少量水银(保持三管中仍有水银),则三管中水银面的位置关系为( )
如图所示,上端封闭的连通器A、B、C 三管中水银面相平,三管横截面积关系为SA>SB>SC,管内水银面上方的空气柱长度为hA>hB>hC,若从下方通过阀门K流出少量水银(保持三管中仍有水银),则三管中水银面的位置关系为( )| A.A管内最高 | B.C管内最高 | C.一样高 | D.无法确定 |
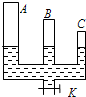

 如图所示,左右两个底部截面均为S的柱形容器竖直放置.左容器足够高,上端敞开,大气压强为p0,右容器上端封闭.两个容器的下端由可忽略容积的细管连通.容器内两个活塞A、B的重力均为0.1p0S,忽略摩擦.初始时,两个活塞A、B下方封有高度均为h的氮气,B上方封有高度为h的氢气.温度为T0=273K,系统处于平衡状态.现用外力将活塞A固定,将系统的底部浸入恒温热水槽中,使氮气温度升高到与水温相同,保持氢气的温度不变,再次平衡时,氢气柱高度变为0.8h.求:
如图所示,左右两个底部截面均为S的柱形容器竖直放置.左容器足够高,上端敞开,大气压强为p0,右容器上端封闭.两个容器的下端由可忽略容积的细管连通.容器内两个活塞A、B的重力均为0.1p0S,忽略摩擦.初始时,两个活塞A、B下方封有高度均为h的氮气,B上方封有高度为h的氢气.温度为T0=273K,系统处于平衡状态.现用外力将活塞A固定,将系统的底部浸入恒温热水槽中,使氮气温度升高到与水温相同,保持氢气的温度不变,再次平衡时,氢气柱高度变为0.8h.求:(12分)如图所示,一连通器与贮有水银的瓶M通过软管相连,连通器的两支上端封闭、粗细均匀、内径相同的直管A和B竖直放置,管内水银的上方均封有空气。A、B两管内水银面的高度差为h cm、空气柱的长度均为2h cm。已知当空气的温度都为T0 K时,A管内空气的压强与3h cm高的水银柱产生的压强相等。现使两管内空气柱的温度都升高到1.5T0 K,同时调节M的高度,使B管中的水银面的高度不变。求:
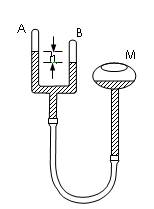
(1)此时B管中气体的压强;
(2)流入A管的水银柱的长度。
一.(20分)填空题.
1、右,大 2、 2(M - ),逐渐减小 3、等于,
4、45°,1:4 5、,
二.(40分)选择题.
6
7
8
9
10
11
12
13
14
D
D
A
B
C
AC
BCD
AD
BD
 三.(30分)实验题.
三.(30分)实验题.
15.(5分)BD
16.(6分)(1)如右图 (2)10Hz (3)
17.(6分)(1)“加入热水后就立即记录一次压强和温度的数值”是错误的,应该是“加入热水后,在气体状态稳定后再记录压强和温度的数值”(指出错误即可得分)
(2)p= t+p1 (3)B
 18.(4分)(1)mvt2 -mv02(1分)
18.(4分)(1)mvt2 -mv02(1分)
(2)变大,变小(2分)
(3)估算图线下方的面积,其大小即为磁力在这一过程 所做功大小(1分)
19.(9分)(1)(如右图)(2分)
(2)BD (3分) (3)0.6,0.6 (4分)
四.(60分)计算题.(各计算题均实行不重复扣分的原则,物理量答案必须有相应的单位)
20.(10分)(1)气体从状态 I 到状态 II::= (2分)
p2 = = = 1.65×105 Pa(3分)
(2)气体从状态 II 到状态 III :p2V2 = p3V3 (2分)
p3 = = = 1.1×105 (Pa)(3分)
21.(12分)(1)弹丸从A到C:t== s=0.6s(1分)
A点到C点的水平距离s = v0t =8.0×
(2)弹丸到C的速度方向与水平方向的夹角为tgθ = = = =(1分)
vC=== m/s =
弹丸与塑料块在C点具有的相同速度vC’=vC=
分析弹丸与塑料块从C点返回到C点的整个过程,根据动能定理有:
-μmgcosθ×2×=0-mvC’2(2分)可得动摩擦因数μ==0.125(1分)
(3)根据牛顿第二定律,下滑时由 a1=gsinθ-μgcosθ可得a1=
由= vC’ t1+a1 t12可解得t1=0.17s(1分)
上滑时由 a1=gsinθ+μgcosθ可得a2=
由=a2t22可解得t2=0.27s(1分)
所以塑料块从被弹丸击中到再次回到C点的时间t= t1+ t2=0.44s(1分)
22.(12分)(1)R2断路,(2分)
电阻R2被烧坏后,电压表读数等于电阻R1的电压大小
可得:R1=4Ω (2分)
(2)根据电路总功率P=εI总
电阻R2被烧坏前后电路总功率之比=
电阻R2被烧坏前I总=(+0.75)A=
电阻R2被烧坏前后电路总功率之比== (4分)
(3)能求出电源电动势E,不能求出电源内阻r(2分)
电阻R2坏前E=1×(R4+r)+0.75×4,电阻R2坏后E=0.8×(R4+r)+3.2
可求出E=4V (2分)
23.(12分) (1) = m (2分) v2=v1= (2分)
(1) = m (2分) v2=v1= (2分)
(2) M黑洞=
对地球:v2地球=;对黑洞:v2黑洞=> c(c为光速)(1分)
= = ≥ (2分)
R黑洞≤ = m=
(3)R恒星=248×109 R地球,M恒星=(248×109)
v2恒星== =
=11. 2×103×248×
所以不能被我们看见 (1分)
24.(14分)(1)通过cd棒的电流方向 d→c(1分)
区域I内磁场方向为垂直于斜面向上(1分)
(2)对cd棒,F安=BIl=mgsinθ所以通过cd棒的电流大小I = (1分)
当ab棒在区域II内运动时cd棒消耗的电功率P=I2R=(1分)
(3)ab棒在到达区域II前做匀加速直线运动,a==gsinθ
cd棒始终静止不动,ab棒在到达区域II前、后,回路中产生的感应电动势不变,则ab棒在区域II中一定做匀速直线运动
可得;=Blvt =Blgsinθt x 所以t x=(2分)
ab棒在区域II中做匀速直线运动的速度vt=
则ab棒开始下滑的位置离EF的距离h= a t x2+
(4) ab棒在区域II中运动的时间t2==(1分)
ab棒从开始下滑至EF的总时间t= t x+t2=2 ε=Blvt =Bl(2分)
ab棒从开始下滑至EF的过程中闭合回路中产生的热量:Q=εIt=4mglsinθ(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com