
题目列表(包括答案和解析)
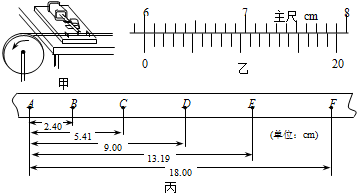 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β.我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出)
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应时间△t的比值定义为角加速度β.我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验:(打点计时器所接交流电的频率为50Hz,A、B、C、D…为计数点,相邻两计数点间有四个点未画出) 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应之间△t的比值定义为角加速度β(即β=
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应之间△t的比值定义为角加速度β(即β=| △ω | △t |
| x2-x1 |
| (n-1) Tr |
| x2-x1 |
| (n-1) Tr |

 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应之间△t的比值定义为角加速度β(即ρ=
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,圆盘加速转动时,角速度的增加量△ω与对应之间△t的比值定义为角加速度β(即ρ=| △? | △t |
 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动时的角速度.
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动.用下面的方法测量它匀速转动时的角速度.| L |
| nTr |
| L |
| nTr |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com