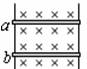
如下图所示，竖直放置的两光滑平行金属导轨放置于垂直于导轨向里的匀强磁场中，两根质量相同的金属棒a、b与导轨接触良好，且可沿导轨自由滑动。先固定a棒、释放b棒，当b棒的速度达到10m/s时，再释放a棒，经过1s时间a棒的速度达到12m/s，则此时金属棒b的速度为（g取10m/s²）

                                                                     

A．12m/s

       B．18m/s

       C．20m/s

       D．22m/s

如下图所示，竖直放置的两根足够长的光滑金属导轨相距为L，导轨的两端分别与电源（串有一滑动变阻器R）、定值电阻和开关K相连。整个空间充满了垂直于导轨平面向外的匀强磁场，磁感应强度的大小为B，一质量为m，电阻不计的金属棒ab横跨在导轨上。已知电源电动势为E，内阻为r，定值电阻的阻值为R₀，不计导轨的电阻。

（1）当K接1时，金属棒ab在磁场中恰好保持静止，求滑动变阻器接入电路的阻值R为多大？

（2）当K接2后，金属棒ab从静止开始下落，下落距离s时达到稳定速度，求该速度的大小；下落s的过程中R₀上产生的热量为多少？

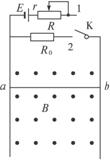
如图所示，竖直放置的两根足够长的光滑金属导轨相距为L，导轨的两端分别与电源（串有一滑动变阻器R）、定值电阻、电容器（原来不带电）和开关K相连。整个空间充满了垂直于导轨平面向外的匀强磁场，其磁感应强度的大小为B。一质量为m，电阻不计的金属棒ab横跨在导轨上。已知电源电动势为E，内阻为r，电容器的电容为C，定值电阻的阻值为R₀，不计导轨的电阻。

（1）当K接1时，金属棒ab在磁场中恰好保持静止，则滑动变阻器接入电路的阻值R多大？

（2）当K接2后，金属棒ab从静止开始下落，下落距离s时达到稳定速度，则此稳定速度的大小为多大？下落s的过程中所需的时间为多少？

（3）先把开关K接通2，待ab达到稳定速度后，再将开关K接到3。试通过推导，说明ab棒此后的运动性质如何？求ab再下落距离s时，电容器储存的电能是多少？（设电容器不漏电，此时电容器还没有被击穿）

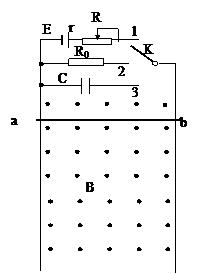
如图所示，竖直放置的两根足够长的光滑金属导轨相距为L，导轨的两端分别与电源（串有一滑动变阻器R）、定值电阻、电容器（原来不带电）和开关K相连。整个空间充满了垂直于导轨平面向外的匀强磁场，其磁感应强度的大小为B。一质量为m，电阻不计的金属棒ab横跨在导轨上。已知电源电动势为E，内阻为r，电容器的电容为C，定值电阻的阻值为R₀，不计导轨的电阻。

（1）当K接1时W#W$W%.K**S*&5^U，金属棒ab在磁场中恰好保持静止，则滑动变阻器接入电路的阻值R多大？

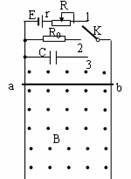（2）当K接2后，金属棒ab从静止开始下落，下落距离s时达到稳定速度，则此稳定速度的大小为多大？下落s的过程中所需的时间为多少？

（3）若在将ab棒由静止释放的同时，将电键K接到3。试通过推导说明ab棒此后的运动性质如何？求ab再下落距离s时，电容器储存的电能是多少？（设电容器不漏电，此时电容器还没有被击穿）

如图所示，竖直放置的两根足够长的光滑金属导轨相距为L，导轨的两端分别与电源（串有一滑动变阻器R）、定值电阻、电容器（原来不带电）和开关K相连．整个空间充满了垂直于导轨平面向外的匀强磁场，其磁感应强度的大小为B．一质量为m，电阻不计的金属棒ab横跨在导轨上．已知电源电动势为E，内阻为r，电容器的电容为C，定值电阻的阻值为R，不计导轨的电阻．
（1）当K接1时，金属棒ab在磁场中恰好保持静止，则滑动变阻器接入电路的阻值R为多大？
（2）当K接2后，金属棒ab从静止开始下落，下落距离s时达到稳定速度，则此稳定速度的大小为多大？下落s的过程中所需的时间为多少？
（3）ab达到稳定速度后，将开关K突然接到3，试通过推导，说明ab作何种性质的运动？求ab再下落距离s时，电容器储存的电能是多少？（设电容器不漏电，此时电容器没有被击穿）