
题目列表(包括答案和解析)
若二项式![]() 的展开式中所有二项式系数的和等于256,则展开式中含x3的项为 .
的展开式中所有二项式系数的和等于256,则展开式中含x3的项为 .
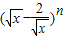 的展开式中所有二项式系数的和等于256,则展开式中含x3的项为 .
的展开式中所有二项式系数的和等于256,则展开式中含x3的项为 . 的展开式中,含x3的项系数等于 .
的展开式中,含x3的项系数等于 . 的展开式中,含x3的项系数等于 .
的展开式中,含x3的项系数等于 .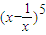 的展开式中,含x3的项系数等于 .
的展开式中,含x3的项系数等于 .一、选择题:(共8题,每小题5分,满分40分)
题号
1
2
3
4
5
6
7
8
答案
A
C
D
C
A
D
B
B
二、填空题:(每题5分,共30分)
9.
8 10.
60 11. 8
12. 
13.
10或0(答对一个给3分) 14.  15.
15. 
三、解答题(本大题共6小题,共80分)
16.(本题满分12分)
解:(Ⅰ)  =
= ……1分
……1分
 =
= ……2分
……2分
∵
 ……4分
……4分
 ……6分
……6分
∵ ……7分
……7分
 .……8分
.……8分
(Ⅱ)在 中,
中, ,
, ,
,
 ……9分
……9分
由正弦定理知: ……10分
……10分

 =
= .
.


 ……12分
……12分
17. 本题满分12分
解:(Ⅰ)由  知
知 是方程
是方程 的两根,注意到
的两根,注意到 得
得  .……2分
.……2分

 得
得 .
.


 等比数列.
等比数列. 的公比为
的公比为 ,
, ……4分
……4分
(Ⅱ) ……5分
……5分
 ……7分
……7分
 数列
数列 是首项为3,公差为1的等差数列. ……8分
是首项为3,公差为1的等差数列. ……8分
(Ⅲ) 由(Ⅱ)知数列 是首项为3,公差为1的等差数列,有
是首项为3,公差为1的等差数列,有
 ……
…… =
= ……
……
= ……10分
……10分
∵

 ,整理得
,整理得 ,解得
,解得 .
. ……11分
……11分
 的最大值是7. ……12分
的最大值是7. ……12分
18. 本题满分14分
解: (Ⅰ)从2种服装商品,2种家电商品,3种日用商品中,选出3种商品一共有 种选法,.选出的3种商品中没有日用商品的选法有
种选法,.选出的3种商品中没有日用商品的选法有 种, 所以选出的3种商品中至少有一种日用商品的概率为
种, 所以选出的3种商品中至少有一种日用商品的概率为 .……4分
.……4分
(Ⅱ)顾客在三次抽奖中所获得的奖金总额是一随机变量,设为X,其所有可能值为0,  ,2
,2 ,3
,3 .……6分
.……6分
X=0时表示顾客在三次抽奖中都没有获奖,所以 ……7分
……7分
同理可得 ……8分
……8分
 ……9分
……9分
 ……10分
……10分
于是顾客在三次抽奖中所获得的奖金总额的期望值是 .……12分
.……12分
要使促销方案对商场有利,应使顾客获奖奖金总额的期望值不大于商场的提价数额,因此应有 ,所以
,所以 , …… 13分
, …… 13分
故商场应将中奖奖金数额最高定为100元,才能使促销方案对商场有利. …… 14分
19.本题满分14分
.解:(Ⅰ) 证明:方法一)连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,∴ //
// ,同理
,同理 //
// ,
,  //
// 
 四边形EFOG是平行四边形,
四边形EFOG是平行四边形,  平面EFOG. ……3分
平面EFOG. ……3分
又在三角形PAC中,E,O分别为PC,AC的中点, PA//EO……4分
PA//EO……4分
 平面EFOG,PA
平面EFOG,PA 平面EFOG, ……5分
平面EFOG, ……5分
 PA//平面EFOG,即PA//平面EFG. ……6分
PA//平面EFOG,即PA//平面EFG. ……6分
方法二) 连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,∴ //
// ,同理
,同理 //
//
 又
又 //AB,
//AB, //
//
 平面EFG//平面PAB, ……4分
平面EFG//平面PAB, ……4分
又PA 平面PAB,
平面PAB, 平面EFG. ……6分
平面EFG. ……6分
方法三)如图以D为原点,以
为方向向量建立空间直角坐标系 .
.
则有关点及向量的坐标为:

 ……2分
……2分
设平面EFG的法向量为

取 .……4分
.……4分
∵ ,……5分
,……5分
又 平面EFG.
平面EFG.
 AP//平面EFG. ……6分
AP//平面EFG. ……6分
(Ⅱ)由已知底面ABCD是正方形

 ,又∵
,又∵ 面ABCD
面ABCD

又
 平面PCD,
平面PCD, 向量
向量 是平面PCD的一个法向量,
是平面PCD的一个法向量,  =
= ……8分
……8分
又由(Ⅰ)方法三)知平面EFG的法向量为 ……9分
……9分
 ……10分
……10分
结合图知二面角 的平面角为
的平面角为 ……11分
……11分
(Ⅲ) ……14分
……14分
20. 本题满分14分
(Ⅰ)由题意可得点A,B,C的坐标分别为 .……1分
.……1分
设椭圆的标准方程是 .……2分
.……2分
则 ……4分
……4分
 .……5分
.……5分
 椭圆的标准方程是
椭圆的标准方程是 ……6分
……6分
(Ⅱ)由题意直线的斜率存在,可设直线 的方程为
的方程为 .……7分
.……7分
 设M,N两点的坐标分别为
设M,N两点的坐标分别为
联立方程:
消去 整理得,
整理得,
有 ……9分
……9分
若以MN为直径的圆恰好过原点,则 ,所以
,所以 ,……10分
,……10分
所以, ,
,
即
所以,
即 ……11分 得
……11分 得 ……12分
……12分
所以直线 的方程为
的方程为 ,或
,或 .……13分
.……13分
所以存在过P(0,2)的直线 :
: 使得以弦MN为直径的圆恰好过原点. ……14分
使得以弦MN为直径的圆恰好过原点. ……14分
21: 本题满分14分
(Ⅰ)
……2分
 ……4分
……4分
(Ⅱ)
(?)0<t<t+2< ,t无解;……5分
,t无解;……5分
(?)0<t< <t+2,即0<t<
<t+2,即0<t< 时,
时, ;……7分
;……7分
(?)
 ,即
,即 时,
时, ,
, ……9分
……9分
 ……10分
……10分
(Ⅲ)由题意:
即

可得 ……11分
……11分
设 ,
,
则 ……12分
……12分
令 ,得
,得 (舍)
(舍)
当 时,
时, ;当
;当 时,
时, 
 当
当 时,
时, 取得最大值,
取得最大值, 
 =-2……13分
=-2……13分
 .
.
 的取值范围是
的取值范围是 .……14分
.……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com