已知正四棱柱ABCD-A₁B₁C₁D₁，AB=1，AA₁=2,点E为CC₁中点,点F为BD₁中点.

(1)证明:EF为BD₁与CC₁的公垂线(即证EF与BD₁、CC₁都垂直);

(2)求点D₁到面BDE的距离.

已知正四棱柱ABCD—A₁B₁C₁D₁的底面边长AB=6，侧棱长，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，则有以下结论：

①PE长的最大值是9；

②三棱锥P—EBC的最大值是[]

③存在过点E的平面，截球O的截面面积是；

④三棱锥P—AEC₁体积的最大值是20。

其中正确结论的是           。（写出所有正确结论的序号）

已知正四棱柱ABCD－A₁B₁C₁D₁中，AA₁=2AB，E为AA₁中点，则异面直线BE与CD₁所形成角的余弦值为

A. 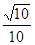            B.        C.             D.