(本小题满分12分)

甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：

甲    82    81    79    78    95    88    93    84

乙    92    95    80    75    83    80    90    85

(1)用茎叶图表示这两组数据；若将频率视为概率，对甲学生在培训后参加的一次数学竞赛成绩进行预测，求甲的成绩高于80分的概率；

(2)现要从中选派一人参加数学竞赛，从统计学的角度(在平均数、方差或标准差中选两个)考虑，你认为选派哪位学生参加合适？请说明理由．

标准差公式：．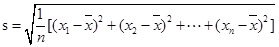

(本小题满分12分)甲、乙二名射击运动员参加第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):

(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;

(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.

(本小题满分12分) 甲、乙两人参加某电视台举办的答题闯关游戏，按照规则，

甲先从道备选题中一次性抽取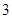道题独立作答，然后由乙回答剩余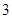题，每人答对其中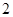

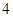题就停止答题，即闯关成功．已知在道备选题中，甲能答对其中的道题，乙答对每道题

的概率都是．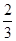

（Ⅰ）求甲、乙至少有一人闯关成功的概率；

（Ⅱ）设甲答对题目的个数为ξ，求ξ的分布列及数学期望．

(本小题满分12分)

甲、乙两名射击运动员，甲射击一次命中10环的概率为，乙射击一次命中10环的概率为s，若他们各自独立地射击两次，设乙命中10环的次数为ξ，且ξ的数学期望Eξ=，表示甲与乙命中10环的次数的差的绝对值.

    (1)求s的值及的分布列，   (2)求的数学期望.

(本小题满分12分) 甲、乙、丙三人在同一办公室工作，办公室里有一部电话机，设经该机打进的电话打给甲、乙、丙的概率依次为若在一段时间内打进三个电话，

且各个电话相互独立，求：

（1）这三个电话是打给同一个人的概率；

（2）这三个电话中恰有两个是打给同一个人的概率.