本小题满分12分）

                        对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：

（Ⅰ）求出表中及图中的值；

（Ⅱ）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间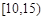内的人数；

（Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间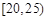内的概率．

（本小题满分12分）

已知A,B是海面上位于东西方向(B在A东)相距5（3+）海里的两个观测点，现位于A点北偏东45⁰，B点北偏西60⁰的D点有一艘轮船发出求救信号，位于B的南偏西60⁰且与B点相距20海里的C点的救援船立即前往营救，其航行速度为30海里／小时，该救援船到达D点需要多长时间？

（本小题满分12分）为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度（单位：cm）满足关系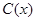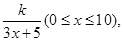： =若不建隔热层，每年能源消耗费用为8万元．设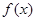为隔热层建造费用与20年的能源消耗费用之和．

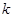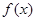    （1）求的值及的表达式;

（2）隔热层修建多厚时，总费用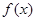达到最小，并求最小值．

（本小题满分12分）

  某公司有一批专业技术人员，对他们进行年龄状况和接受教育程度(学历)的调查，其结果(人数

分布)如下表：

 （1）用分层抽样的方法在35～50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本

      看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率；

（2）在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取个人，其中35岁以

 下48人，50岁以上10人，再从这个人中随机抽取出1人，此人的年龄为50岁以上

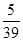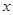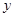 的概率为，求、的值.

（本小题满分12分）

某大学高等数学老师上学期分别采用了两种不同的教学方式对甲、乙两个大一新生班进行教改试验（两个班人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩，得到茎叶图如下：

（Ⅰ）依茎叶图判断哪个班的平均分高？

（Ⅱ）从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学，求成绩为90分的同学被抽中的概率；

（Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的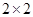列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”

下面临界值表仅供参考：

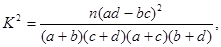（参考公式：其中） 

（Ⅳ）从乙班高等数学成绩不低于85分的同学中抽取2人，成绩不低于90分的同学得奖金100元，否则得奖金50元，记为这2人所得的总奖金，求的分布列和数学期望。