
题目列表(包括答案和解析)
设![]() ,求
,求![]() 的最小值;若
的最小值;若![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
 ,求
,求 的最小值;若
的最小值;若 ,
, ,求
,求 的最大值.
的最大值.![]()
(1)求![]() 的最小值;(2)若
的最小值;(2)若![]() ≥
≥![]() 在
在![]() 内恒成立,求
内恒成立,求![]() 的取值范围
的取值范围

 的最小正周期和单调增区间;
的最小正周期和单调增区间; 时,函数
时,函数 的最大值与最小值的和
的最大值与最小值的和 ,求
,求
、⑴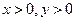 ,且
,且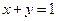 ,求
,求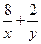 的最小值;
的最小值;
⑵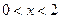 ,求
,求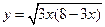 的最大值。
的最大值。
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
答案
C
B
C
D
C
A
C
B
A
D
C
提示与分析:
1. ,故选C。
,故选C。
2.易知p成立,m<3,q成立,2<m< ,从而p成立
,从而p成立 成立,故选B。
成立,故选B。
3.选C
4.由已知得 即
即 ,得
,得 ,故选D。
,故选D。
5.易知 ,故选C。
,故选C。
6. ,作图知选A。
,作图知选A。
7.选C。由题: 。
。
8.设球半径为R,由 ,由
,由 知,三棱锥顶点S爱底面ABC内的摄影D是△ABC的外心,又∠ACB=90°,∴D是AB的中点,点O到ABC的距离h=OD,设SA=SB=SC=AB=2
知,三棱锥顶点S爱底面ABC内的摄影D是△ABC的外心,又∠ACB=90°,∴D是AB的中点,点O到ABC的距离h=OD,设SA=SB=SC=AB=2 ,可得
,可得
 ,或h=10(舍),故选B。
,或h=10(舍),故选B。
9.由题设易知M是PF的中点,设椭圆右焦点为 ,由
,由 知,
知, =8,
=8, ,又易知该椭圆的离心率
,又易知该椭圆的离心率 ,再由椭圆第二定义得,点P到椭圆左准线的距离
,再由椭圆第二定义得,点P到椭圆左准线的距离 ,故选A。
,故选A。
10.由 ,∴
,∴ 故选D。
故选D。
11.由题设知 是周期为2的周期函数,由
是周期为2的周期函数,由 时,
时, ,可作出
,可作出 再R上的简图,又
再R上的简图,又 是偶函数,再作出简图,则可确定两图像的交点个数,故选C。
是偶函数,再作出简图,则可确定两图像的交点个数,故选C。
二、填空题
12.112 13.9 14.32 15.①②④
提示与分析:
12.令 得
得 ,再分别令
,再分别令 得两式,再相加可得
得两式,再相加可得 ,从而得知
,从而得知 。
。
13.由题得: ,
, 得:
得: ,而
,而 可看作是单位圆上的点(m,n)到点(2,0)的距离,则易知,
可看作是单位圆上的点(m,n)到点(2,0)的距离,则易知, 的最大值为9.
的最大值为9.
14.由题设知, 又0<q<1则得
又0<q<1则得 ,∴
,∴
15.如图,①知直线BC与面 所成的角即为∠
所成的角即为∠ ,故①正确。
,故①正确。
②易知四面体 在四个侧面的摄影图形面积均最小,为正方形面积之半,故②正确
在四个侧面的摄影图形面积均最小,为正方形面积之半,故②正确
③点M到平面 的距离,即为点
的距离,即为点 到平面
到平面 的距离。其等于
的距离。其等于 ,故③不正确。
,故③不正确。
④易知BM与 所成的角,即为BM与
所成的角,即为BM与 所成的角,设∠
所成的角,设∠ ∠
∠ 易知
易知 ,
, ,即
,即 ,故④正确。
,故④正确。
三、解答题
16.(1)由题设知:
再由余弦定理得:
当且仅当 时取等号,故所求B的取值范围是
时取等号,故所求B的取值范围是 (3分)
(3分)
(2)∵ ,∴
,∴ ,
,
∴0<b ,当且仅当
,当且仅当 时,
时,
∴
∴ (6分)
(6分)
(3)由(1)(2)易知,当△ABC的面积S最大时,△ABC是边长为2的正△,此时易知 ∠
∠ ∠
∠
 在△AGM中,由正弦定理得:
在△AGM中,由正弦定理得:
则
在△AGN中,同理可得:
 (10分)
(10分)
∴ (或用降次公式化简)
(或用降次公式化简)


 (12分)
(12分)
17.解法一:
(1)由PB⊥面ABCD,CD⊥PD知CD⊥BD
 在直角梯形ABCD中,AD⊥AB,AB=AD=3,
在直角梯形ABCD中,AD⊥AB,AB=AD=3,
∴BD= ,BC=6
,BC=6
取BC的中点F,连结AF,则AF∥CD,
∴PA与CD所成的角就是∠PAF (4分)
连PF由题设易知AF=PF=PA= ,
,
∴∠PAF=60°即为所求 (6分)
(2)连AC交BD于G,连EG,易知 ,
,
又 ∴
∴ ,∴PC∥EG,又EG
,∴PC∥EG,又EG 面EBD,∴PC∥面EBD (10分)
面EBD,∴PC∥面EBD (10分)
(3)∵PB⊥面ABCD,∴AD⊥PB,
又AD⊥AB,∴AD⊥面EAB
作AH⊥BE于H,连DH,则DH⊥BE, (12分)
在△AEB中,易求得BE= ,
,
在 △DAH中,
△DAH中, ∠
∠
即所求二面角的大小为 (14分)
(14分)
 解法二:(1)如图建立空间直角坐标系
解法二:(1)如图建立空间直角坐标系 ,设
,设

则A(0,3,0),P(0,0,3)D(3,3,0),C( ,0,0),
,0,0), =
=
∵ ,∴
,∴ ,
,
即:3(3- )+9=0
)+9=0 (2分)
(2分)
∴
∴
∴ ,即异面直线PA与CD所成的交为60°
(6分)
,即异面直线PA与CD所成的交为60°
(6分)
(2)设平面BED的法向量为 ∵
∵
由 得
得
 ,∴
,∴ (12分)
(12分)
又由(1)知 ,∴
,∴ ,∴PC∥面EBD (10分)
,∴PC∥面EBD (10分)
(3)由(2)知
又平面ABE的法向量 ,
,
故所求二面角的大小为 (14分)
(14分)
18.(1)在第一环节中,乙选手从6道题目中任选3道至少有1道操作题的概率
 (4分)
(4分)
(2)在第二环节中,甲抢到的题目多于乙选手而不多于丙选手的情况有以下三种:
甲、乙、丙三位选手抢到的题目的个数分别为1,0,4;2,0,3;2,1,2,
故所求的概率


(8分)
(3)在第三个环节中,就每一次答题而言,丙选手得分是一个随机变量 ,
,
若选A类题,其得分的期望是 (分)
(分)
若选B类题,其得分的期望是 (分)
(分)
若选C类题,其得分的期望是 (分)
(分)
由于 >
> =
= ,故丙应选B类得分的切望值更大。(12分)
,故丙应选B类得分的切望值更大。(12分)
19.(1)依题意可得:
(4分)
(2)由

当 时,
时, ,则
,则
∴ ,∴
,∴
即第 次操作后溶液的浓度为
次操作后溶液的浓度为 (9分)
(9分)
(3)由(2)可得:
则
由错位相减法可求得:

故所求 (13分)
(13分)
20.(1)由 <0,
<0, >
> ,∴
,∴
又 >
> <
< ,∴
,∴
从而有  (4分)
(4分)
(2)由(1)可知,
故 ,则
,则
令 >
> ∵
∵ >
> 得
得 >
> ,∴
,∴ >
>
令 <
< ∵
∵ >
> ,解得
,解得 <
< <
<
列表:

(0,1)
1
(1,+∞)

-
0
+

↓
0
↑
即  在
在 处有最小值0 (8分)
处有最小值0 (8分)
(3)由 易知
易知 时,
时, <
<
∴ 为减函数,其最小值为1
为减函数,其最小值为1
令 在
在 上单增,其最大值为
上单增,其最大值为
依题意得:
又 >
> ∴
∴ <
< (14分)
(14分)
21.(1)由题设及平面几何知识得: <
< ,
,
∵动点P的轨迹是以A、B为交点的双曲线右支,
由
故所求P点的轨迹方程为: (4分)
(4分)
(2)易知 直线 恒过双曲线焦点B(3,0)
恒过双曲线焦点B(3,0)
设该直线与双曲线右支相交于
由双曲线第二定义知,
又 ∴
∴ ,则
,则 ,
,
由 得
得 ,从而易知,仅当
,从而易知,仅当 时,
时, 满足
满足
故所求 (8分)
(8分)
(3)设 ,且p分有向线段
,且p分有向线段 所成的比为
所成的比为 ,
,
则 ,
, ,
,
又点 在双曲线
在双曲线 上,∴
上,∴
化简得:
又

∴ (11分)
(11分)
令
∵ 在
在 上单减,在
上单减,在 上单增,
上单增,
又 ,∴
,∴ 在
在 上单减,在
上单减,在 上单增,∴
上单增,∴
又
 ,∴
,∴
故所求 的最小值为9,最大值为
的最小值为9,最大值为 。 (14分)
。 (14分)
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
| ||||||||||||||||||||||||||||||||||