
题目列表(包括答案和解析)
(08年安徽皖南八校联考)(本小题满分14分)
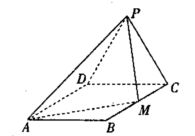 如图所示,边长为2的等边△
如图所示,边长为2的等边△![]() 所在的平面垂直于矩形
所在的平面垂直于矩形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥
⊥![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
(08年安徽皖南八校联考理)(本小题满分14分)
数列![]() 的首项
的首项![]() =1,前
=1,前![]() 项和为
项和为![]() 满足
满足![]() (常数
(常数![]() ,
,![]() ).
).
(1)求证:数列![]() 是等比数列.
是等比数列.
(2)设数列![]() 的公比为
的公比为![]() ,作数列
,作数列![]() ,使
,使![]() ,
,![]() (
(![]() 2,3,
2,3,
4,…),求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,若存在
,若存在![]() ,且
,且![]() ;
;
使![]() (
(![]() …
…![]() )
)![]() ,试求
,试求![]() 的最小值.
的最小值.
(08年安徽信息交流文)(本小题满分14分)甲、乙两个容器中分别装有浓度为5%、15%的某种溶液500ml,现同时从甲、乙两个容器中各倒出200ml后,再分别倒入对方容器搅匀,这称作是一次调和,记![]() ,
,![]() ,经过
,经过![]() 次调和后,甲、乙两个容器中的溶液浓度分别为
次调和后,甲、乙两个容器中的溶液浓度分别为![]() .
.
(1)试用![]() ,
,![]() 表示
表示![]() 和
和![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)记![]() ,证明:
,证明:![]() 。
。
(08年广东卷理)(本小题满分14分)设![]() ,函数
,函数 ,
,![]() ,
,![]() ,试讨论函数
,试讨论函数![]() 的单调性.
的单调性.
(08年广东卷)(本小题满分14分)设![]() ,椭圆方程为
,椭圆方程为![]() ,抛物线方程为
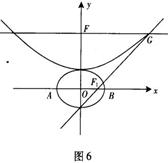
,抛物线方程为![]() .如图6所示,过点
.如图6所示,过点![]() 作
作![]() 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为![]() ,已知抛物线在点
,已知抛物线在点![]() 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点![]() .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设![]() 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com