
题目列表(包括答案和解析)
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
【解析】第一问当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
第二问当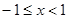 时,
时, ,令
,令 得
得 ,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
第三问假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设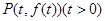 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当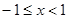 时,
时, ,令
,令 得
得
当 变化时,
变化时,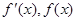 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
极小值 |
单调递增 |
极大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当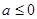 时,
时,  ,
, 最大值为0;
最大值为0;
当 时,
时,  在
在 上单调递增。∴
上单调递增。∴ 在
在 最大值为
最大值为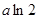 。
。
综上,当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为2;
上的最大值为2;
当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为
上的最大值为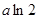 。
。
(Ⅲ)假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设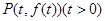 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
若 ,则
,则 代入(*)式得:
代入(*)式得:
即 ,而此方程无解,因此
,而此方程无解,因此 。此时
。此时 ,
,
代入(*)式得:  即
即 (**)
(**)
令
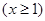 ,则
,则
∴ 在
在 上单调递增, ∵
上单调递增, ∵  ∴
∴ ,∴
,∴ 的取值范围是
的取值范围是 。
。
∴对于 ,方程(**)总有解,即方程(*)总有解。
,方程(**)总有解,即方程(*)总有解。
因此,对任意给定的正实数 ,曲线
,曲线 上存在两点P、Q,使得
上存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上
轴上
你以前听说过“鸡兔同笼”问题吗?这个问题,是我国古代著名趣题之一.大约在1 500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?
你会解答这个问题吗?你想知道《孙子算经》中是如何解答这个问题的吗?
解答思路是这样的:假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”.这样,(1)鸡和兔的脚的总数就由94只变成了47只;(2)如果笼子里有一只兔子,则脚的总数就比头的总数多1.因此,脚的总只数47与总头数35的差,就是兔子的只数,即47-35=12(只).显然,鸡的只数就是35-12=23(只)了.
这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.这种思维方法叫化归法.
化归法就是在解决问题时,先不对问题采取直接的分析,而是将题中的条件或问题进行变形,使之转化,直到最终把它归成某个已经解决的问题.
1.古代《孙子算经》就有这么好的解法——化归法,这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.对此,谈谈你的看法.
2.我国古代数学研究一直处于领先地位,现在有所落后了,对此,我们不应只感叹古人的伟大,而更应该树立为科学而奋斗终身的信心,同学们,你们准备好了吗?
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成.组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料.蜂房的巢壁厚0.073毫米,误差极小.
丹顶鹤总是成群结队迁飞,而且排成“人”字形.“人”字形的角度是110度.更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?
蜘蛛结的“八卦”形网,是既复杂又美丽的八角形几何图案,人们即使用直尺的圆规也很难画出像蜘蛛网那样匀称的图案.
冬天,猫睡觉时总是把身体抱成一个球形,这其间也有数学,因为球形使身体的表面积最小,从而散发的热量也最少.
真正的数学“天才”是珊瑚虫.珊瑚虫在自己的身上记下“日历”,它们每年在自己的体壁上“刻画”出365条斑纹,显然是一天“画”一条.奇怪的是,古生物学家发现3亿5千万年前的珊瑚虫每年“画”出400幅“水彩画”.天文学家告诉我们,当时地球一天仅21.9小时,一年不是365天,而是400天.
1.同学们,大自然中有许多有关数学的奥妙,许多现象有意无意地应用着数学,对于这些现象你有什么看法吗?请你谈谈你对大自然中的数学现象的认识.
2.把你发现的大自然中的数学问题告诉你的同学和老师,让他们也分享一下你认识大自然的乐趣.
1.解:由题意可知A=(-2,3),B=(0,4),∴ =
= .
.
2.解:∵ =3x2,∵在(a,a3)处切线为y-a3=
=3x2,∵在(a,a3)处切线为y-a3= ),切线与直线x=a交于(a,a3),∴曲线
),切线与直线x=a交于(a,a3),∴曲线 处的切线与x轴、直线
处的切线与x轴、直线 所围成的三角形的面积为S=
所围成的三角形的面积为S= ,令S=
,令S= ,解得a=±1.
,解得a=±1.
3.解:由已知得1-tanαtanβ=tanα-tanβ,∴tanα= .
.
4.解: =
=
5.解:4位乘客进入4节车厢共有256种不同的可能,6位乘客进入各节车厢的人数恰为0,1,2,3的方法共有 ,∴这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为
,∴这6位乘客进入各节车厢的人数恰好为0,1,2,3的概率为 .
.
6.解:①菱形不可能,如果这个四边形是菱形,这时菱形的一条对角线垂直抛物线的对称轴,这时四边形的必有一个顶点在抛物线的对称轴上(非抛物线的顶点); ④平行四边形,也不可能,因为抛物上四个点组成的四边形最多有一组对边平行.故连接抛物线上任意四点组成的四边形可能是②③⑤.
7. 解:复数 =
= 。
。
8. 解:
 。
。
9. 解:已知
 ,
, ,
, ,∴
,∴  ,
, ,
,
则
 =
=
=
10. 解:在数列 中,若
中,若 ,∴
,∴  ,即{
,即{ }是以
}是以 为首项,2为公比的等比数列,
为首项,2为公比的等比数列, ,所以该数列的通项
,所以该数列的通项

 .
.
11.解:设 ,函数
,函数 有最大值,∵
有最大值,∵ 有最小值,∴ 0<a<1, 则不等式
有最小值,∴ 0<a<1, 则不等式 的解为
的解为 ,解得2<x<3,所以不等式的解集为
,解得2<x<3,所以不等式的解集为 .
.
 12.解:已知变量
12.解:已知变量 满足约束条件
满足约束条件 在坐标系
在坐标系
中画出可行域,如图为四边形ABCD,其中A(3,1), ,
,
目标函数 (其中
(其中 )中的z表示斜率为-a的直线系中的
)中的z表示斜率为-a的直线系中的
截距的大小,若仅在点 处取得最大值,则斜率应小于
处取得最大值,则斜率应小于 ,即
,即
 ,所以
,所以 的取值范围为(1,+∞)。
的取值范围为(1,+∞)。
13.【答案】:
【分析】:
 14.【答案】:7
14.【答案】:7
【分析】:画出可行域,当直线过点(1,2)时,

15.【答案】:
【分析】: 恒成立,
恒成立,
 恒成立,
恒成立, 
16.【答案】:18
【分析】: 和
和 是方程
是方程 的两根,故有:
的两根,故有:
 或
或 (舍)。
(舍)。

17.【答案】:25
【分析】:所有的选法数为 ,两门都选的方法为
,两门都选的方法为 。
故共有选法数为
。
故共有选法数为
18.【答案】:
【分析】:


代入 得:
得:
设
又

19.解: ,
,

20.解:
 又
又  点在x=0处连续,
点在x=0处连续,
所以 即
即 故
故
21.解:


22.解:  ,
,

 23.解:设圆心
23.解:设圆心 ,直线
,直线 的斜率为
的斜率为 , 弦AB的中点为
, 弦AB的中点为 ,
, 的斜率为
的斜率为 ,
, 则
则 ,所以
,所以
 由点斜式得
由点斜式得
24. 解: 则底面共
则底面共 ,
,
 ,
,
 ,由分类计数原理得上底面共
,由分类计数原理得上底面共 ,由分步类计数原理得共有
,由分步类计数原理得共有 种
种
25.解析:本小题主要考查三点共线问题。


 (舍负).
(舍负).
26.解析:本小题主要考查椭圆的第一定义的应用。依题直线 过椭圆的左焦点
过椭圆的左焦点 ,在
,在 中,
中, ,又
,又 ,∴
,∴
27.解析:本小题主要考查三角形中正弦定理的应用。依题由正弦定理得:
 ,即
,即 ,
,
∴
 28.解析:本小题主要考查球的内接几何体体积计算问题。其关键是找出
28.解析:本小题主要考查球的内接几何体体积计算问题。其关键是找出
球心,从而确定球的半径。由题意,三角形DAC,三角形DBC都
是直角三角形,且有公共斜边。所以DC边的中点就是球心(到
D、A、C、B四点距离相等),所以球的半径就是线段DC长度的一半。
29.解析:本小题主要考查二次函数问题。对称轴为 下方图像翻到
下方图像翻到 轴上方.由区间[0,3]上的最大值为2,知
轴上方.由区间[0,3]上的最大值为2,知 解得
解得 检验
检验 时,
时,
 不符,而
不符,而 时满足题意.
时满足题意.
30.解析:本小题主要考查排列组合知识。依题先排除1和2的剩余4个元素有
种方案,再向这排好的4个元素中插入1和2捆绑的整体,有 种插法,
种插法,
∴不同的安排方案共有 种。
种。
31.解析:本小题主要考查线性规划的相关知识。由 恒成立知,当
恒成立知,当 时,
时,
 恒成立,∴
恒成立,∴ ;同理
;同理 ,∴以
,∴以 ,b为坐标点
,b为坐标点
所形成的平面区域是一个正方形,所以面积为1.
32.解析: ,所以
,所以 ,系数为
,系数为 .
.
33.解析:由 得
得 ,所以
,所以 ,表面积为
,表面积为 .
.
34.解析:抛物线的焦点为 ,所以圆心坐标为
,所以圆心坐标为 ,
, ,圆C的方程为
,圆C的方程为 .
.
 35.解析:令
35.解析:令 ,
, ,则
,则
所以 .
.
36.解析:
所以 .
.
37.解析:由已知得 ,单调递减,所以当
,单调递减,所以当 时,
时,
所以 ,因为有且只有一个常数
,因为有且只有一个常数 符合题意,所以
符合题意,所以 ,解得
,解得 ,所以
,所以 的取值的集合为
的取值的集合为 .
.
38.【解】:∵ 展开式中
展开式中 项为
项为

∴所求系数为 故填
故填
【点评】:此题重点考察二项展开式中指定项的系数,以及组合思想;
【突破】:利用组合思想写出项,从而求出系数;
 39.【解】:如图可知:过原心作直线
39.【解】:如图可知:过原心作直线 的垂线,则
的垂线,则 长即为所求;
长即为所求;
∵ 的圆心为
的圆心为 ,半径为
,半径为
点 到直线
到直线 的距离为
的距离为
∴  故
故 上各点到
上各点到 的距离的最小值为
的距离的最小值为
【点评】:此题重点考察圆的标准方程和点到直线的距离;
 【突破】:数形结合,使用点
【突破】:数形结合,使用点 到直线
到直线 的距离距离公式。
的距离距离公式。
40.【解】:如图可知:∵
∴ ∴正四棱柱的体积等于
∴正四棱柱的体积等于

【点评】:此题重点考察线面角,解直角三角形,以及求正四面题的体积;
【突破】:数形结合,重视在立体几何中解直角三角形,熟记有关公式。
41.【解】:∵等差数列 的前
的前 项和为
项和为 ,且
,且
∴ 即
即 ∴
∴
∴ ,
, ,
, 
∴ 故
故 的最大值为
的最大值为 ,应填
,应填
【点评】:此题重点考察等差数列的通项公式,前 项和公式,以及不等式的变形求范围;
项和公式,以及不等式的变形求范围;
【突破】:利用等差数列的前 项和公式变形不等式,利用消元思想确定
项和公式变形不等式,利用消元思想确定 或
或 的范围解答本题的关键;
的范围解答本题的关键;
42.解:
43.解:设 则
则

 ,即
,即
 则
则 是等边三角形,
是等边三角形, ,
,
在 中,
中,
 故
故
44.解:① ,向量
,向量 与
与 垂直
垂直
②



③
 构成等边三角形,
构成等边三角形, 与
与 的夹角应为
的夹角应为
所以真命题只有②。
45.解:分两类:第一棒是丙有 ,第一棒是甲、乙中一人有
,第一棒是甲、乙中一人有
因此共有方案 种
种
46.【答案】 2
【解析】 =
= 则向量
则向量 与向量
与向量 共线
共线
47.【答案】 2
【解析】 ,∴切线的斜率
,∴切线的斜率 ,所以由
,所以由 得
得
48.【答案】
【解析】设A( ,
, )B(
)B( ,
, )由
)由
 ,
, ,(
,( );∴由抛物线的定义知
);∴由抛物线的定义知
【考点】直线与抛物线的位置关系,抛物线定义的应用
49.【答案】两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.
注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.
50.答案:
解析:本小题主要考查求反函数基本知识。求解过程要注意依据函数的定义域进行分段求解以及反函数的定义域问题。
51.答案:
解析:本小题主要考查立体几何球面距离及点到面的距离。设球的半径为 ,则
,则 ,∴
,∴ 设
设 、
、 两点对球心张角为
两点对球心张角为 ,则
,则 ,∴
,∴ ,∴
,∴ ,∴
,∴ 为
为 所在平面的小圆的直径,∴
所在平面的小圆的直径,∴ ,设
,设 所在平面的小圆圆心为
所在平面的小圆圆心为 ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为

52.答案:5
解析:本小题主要考查二项式定理中求特定项问题。依题 对
对 中,只有
中,只有 时,其展开式既不出现常数项,也不会出现与
时,其展开式既不出现常数项,也不会出现与 、
、 乘积为常数的项。
乘积为常数的项。
53.答案:
解析:本小题主要针对考查三角函数图像对称性及周期性。依题 且
且 在区间
在区间 有最小值,无最大值,∴区间
有最小值,无最大值,∴区间 为
为 的一个半周期的子区间,且知
的一个半周期的子区间,且知 的图像关于
的图像关于 对称,∴
对称,∴ ,取
,取 得
得
54.解:由已知得 ,则
,则
55.解:

56.
 57.解:真命题的代号是: BD 。易知所盛水的容积为容器容量的一半,故D正确,于是A错误;水平放置时由容器形状的对称性知水面经过点P,故B正确;C的错误可由图1中容器位置向右边倾斜一些可推知点P将露出水面。
57.解:真命题的代号是: BD 。易知所盛水的容积为容器容量的一半,故D正确,于是A错误;水平放置时由容器形状的对称性知水面经过点P,故B正确;C的错误可由图1中容器位置向右边倾斜一些可推知点P将露出水面。
58.【答案】
【解析】
59.【答案】
【解析】


60.【答案】(-1,2)
【解析】由函数 的图象过点(1,2)得:
的图象过点(1,2)得:  即函数
即函数 过点
过点 则其反函数过点
则其反函数过点 所以函数
所以函数 的图象一定过点
的图象一定过点
61.【答案】 ,
, 
【解析】(1)当a>0时,由 得
得 ,所以
,所以 的定义域是
的定义域是 ;
;
(2) 当a>1时,由题意知 ;当0<a<1时,为增函数,不合;
;当0<a<1时,为增函数,不合;
当a<0时, 在区间
在区间 上是减函数.故填
上是减函数.故填 .
.
62.【答案】 , 6
, 6
【解析】 第二空可分:
第二空可分:
①当
 时,
时,  ;
;
②当 
 时,
时,  ;
;
③当

 时,
时,  ;
;
所以
也可用特殊值法或i和j同时出现6次.
63.解:由余弦定理,原式
64.解:由题意知 所以
所以
 ,所以解集为
,所以解集为 。
。
65.解:依题意 ,所以
,所以


66.解:由观察可知当 ,每一个式子的第三项的系数是成等差数列的,所以
,每一个式子的第三项的系数是成等差数列的,所以 ,
,
第四项均为零,所以 。
。
67.解:令 ,令
,令 得
得
所以 
68. 解:圆心为 ,要没有公共点,根据圆心到直线的距离大于半径可得
,要没有公共点,根据圆心到直线的距离大于半径可得
 ,即
,即 ,
,
69.解:依题可以构造一个正方体,其体对角线就是外接球的直径.
 ,
,
70. 解:①对除法如 不满足,所以排除,
不满足,所以排除,
②取 ,对乘法
,对乘法 , ③④的正确性容易推得。
, ③④的正确性容易推得。
71.【答案】: -1
【分析】: a -2ai-1=a
-2ai-1=a -1-2ai=2i,a=-1
-1-2ai=2i,a=-1
【考点】: 复数的运算
【易错】: 增根a=1没有舍去。
72.【答案】: 0
【分析】: 利用数形结合知,向量a与
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com