（本小题满分12分）甲、乙两人进行一种游戏，两人同时随机地喊出杠、虎、鸡、虫，按照

杠打虎、虎吃鸡、鸡吃虫、虫啃杠的原则决定胜负。 （比如甲喊杠的同时，乙若喊虎则乙输，乙若

喊虫则乙赢，乙若喊杠或鸡则不分胜负。）   若两人同时喊出一次后不分胜负则继续喊下去，直到

分出胜负。

（Ⅰ）喊一次甲就获胜的概率是多少？

（Ⅱ）甲在喊不超过三次的情况下就获胜的概率是多少？

.COM

（本小题满分12分）

甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹。根据以往资料知，甲击中8环，9环，10环的概率分别为0.6，0.3，0.1，乙击中8环，9环，10环的概率分别为0.4，0.4，0.2。

设甲、乙的射击相互独立。

（Ⅰ）求在一轮比赛中甲击中的环数多于乙击中环数的概率；

（Ⅱ）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率。

（本小题满分12分）

甲、乙两人在罚球线投球命中的概率分别为，投中得1分，投不中得0分.

（Ⅰ）甲、乙两人在罚球线各投球一次，求两人得分之和ξ的数学期望；

（Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率；

（本小题满分12分） 甲、乙两人在一场五局三胜制的象棋比赛中，规定甲或乙无论谁先赢满三局就获胜，并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是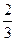，乙取胜的概率为，且每局比赛的胜负是独立的，试求下列问题：
(Ⅰ)比赛以甲3胜1而结束的概率；
(Ⅱ)比赛以乙3胜2而结束的概率；
(Ⅲ)设甲获胜的概率为a，乙获胜的概率为b，求a：b的值.

（本小题满分12分）

甲，乙两人进行射击比赛，每人射击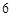次，他们命中的环数如下表：

（Ⅰ）根据上表中的数据，判断甲，乙两人谁发挥较稳定；

（Ⅱ）把甲6次射击命中的环数看成一个总体，用简单随机抽样方法从中抽取两次命中的环数组成一个样本，求该样本平均数与总体平均数之差的绝对值不超过的概率．