（本小题满分14分）

f(x)是定义在R上的奇函数，且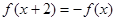，当时，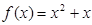

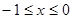（1）求函数的周期   （2）求函数在的表达式 （3）求

(本小题满分14分)函数f(x)＝1－2a－2acosx－2sin²x的最小值为g(a)(a∈R)．

(1)求g(a)；

(2)若g(a)＝，求a及此时f(x)的最大值．

（本小题满分13分）f(x)为定义在R上的偶函数，但x≥0时，y= f(x)的图像是顶点在P(3，4)，且过点A(2，2)的抛物线的一部分。

(1)求函数f(x)在(－∞，0)上的解析式；

(2)求函数f(x)在R上的解析式，并画出函数f(x)的图像；

(3)写出函数f(x)的单调区间

21．(本小题满分14分)

定义数列{a_n}如下：a₁＝2，a_n＋1＝a_n²－a_n＋1，n∈N^*.证明：

(1)对于n∈N^* 恒有a_n＋1＞a_n 成立；

(2)当n∈N^*时，有a_n＋1＝a_na_n－1…a₂a₁＋1成立；

(3)

本小题满分14分）

向量=,x∈.函数f(x)= -|+|

（1）若函数f(x)的最小值为-，求实数的值，并求出f(x)取最小值-时相应的值.

（2）点O为坐标原点，当f(x)取最小值-时，向量=、向量=、,若点是的重心，线段经过点，并绕点转动，分别交边、于点、；设，，  其中，，证明：；