
题目列表(包括答案和解析)
(本小题满分13分)
某化工企业生产某种产品,生产每件产品的成本为3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11 – x)2万件;若该企业所生产的产品能全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a (1≤a≤3).
(Ⅰ)求该企业正常生产一年的利润L (x)与出厂价x的函数关系式; ![]()
![]()
(Ⅱ)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
(本小题满分14分)
某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y( 码 ) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序 号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y( 码 ) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的![]() 联列表:
联列表:
| 高 个 | 非高个 | 合 计 | |
| 大 脚 | |||
| 非大脚 | 12 | ||
| 合 计 | 20 |
(Ⅱ)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:
①抽到12号的概率;②抽到“无效序号(超过20号)”的概率.
(本小题满分12分)
在清明节前,哈市某单位组织员工参加植树祭扫,林管局在植树前为了保证树苗质量,都会对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,量出它们的高度如下:(单位:厘米)
甲:37 21 31 21 28 19 32 23 25 33
乙:10 30 47 27 46 14 26 11 43 46
(1)根据抽测结果画出茎叶图,并根据你所填写的茎叶图对两种树苗高度作比较,写出3个统计结论;
(2)如果认为甲种树苗高度超过30厘米为优质树苗,那么在己抽测的甲种10株树苗中任选两株栽种,记优质树苗的个数为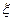 ,求
,求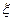 的分布列和期望.
的分布列和期望.
(本小题满分14分)
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:

(I)请画出适当的统计图(茎叶图或频率分布直方图);如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次成绩中各随机抽取一次,求抽取的成绩中至少有一个不高于 12.8秒的概率.
(III)经过对甲、乙两位同学的若干次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,
现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
(本小题满分12分) 第11届全国人大五次会议于20 1 2年3月5日至3月1 4日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和1 4名女记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语.
(Ⅰ)根据以上数据完成以下2×2列联表:
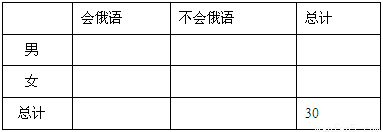
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
(参考公式: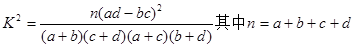
参考数据:

(Ⅱ)已知会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随
机抽取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com