（本小题共12分）





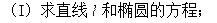
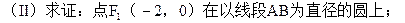
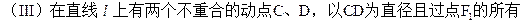
圆中，求面积最小的圆的半径长。

（本小题满分12分）如图是求函数值的一个程序。

    ⑴ 请写出这个函数的表达式；

    ⑵ 根据右图程序，写出输入的值，

       输出函数值的一个算法。

（本小题共12分）

现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表．

（1）由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令” 的态度有差异；

（2)若对在[15，25） ，[25，35）的被调查中各随机选取两人进行追踪调查，记选中的4人中不赞成“楼市限购令”人数为 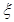，求随机变量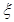的分布列。

附：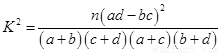

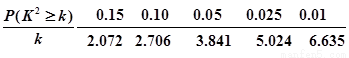
（本小题共12分）将一颗骰子先后抛掷2次，观察向上的点数，求：

（1）两数之和为5的概率；

（2）两数中至少有一个奇数的概率；

（3）以第一次向上点数为横坐标x，第二次向上的点数为纵坐标y的点(x,y)在圆x²+y²=15的内部的概率．

（本小题共12分）

已知函数f(t)= ]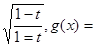

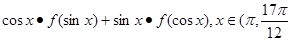（Ⅰ）将函数g(x)化简成Asin(ωx+φ)+B（A＞0，ω＞0，φ∈[0，2π））的形式；

（Ⅱ）求函数g(x)的值域.