1.         （本小题满分12分）

从直线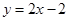：上任意一点引抛物线的两条切线，切点分别为、．

（Ⅰ）求证：直线过定点，并求点的坐标；

（Ⅱ）求三角形面积的最小值．

(本小题满分12分)
在清明节前，哈市某单位组织员工参加植树祭扫，林管局在植树前为了保证树苗质量，都会对树苗进行检测，现从甲、乙两种树苗中各抽测了10株树苗的高度，量出它们的高度如下：(单位：厘米)
甲：37  21  31  21  28  19  32  23  25  33
乙：10  30  47  27  46  14  26  11  43  46
(1)根据抽测结果画出茎叶图，并根据你所填写的茎叶图对两种树苗高度作比较，写出3个统计结论；
(2)如果认为甲种树苗高度超过30厘米为优质树苗，那么在己抽测的甲种10株树苗中任选两株栽种，记优质树苗的个数为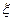，求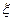的分布列和期望．

．(本小题满分12分)

　　设函数f(x)=lnx－p(x－1)，p∈R.

(Ⅰ)当p=1时，求函数f(x)的单调区间；

(Ⅱ)设函数g(x)=xf(x)+p(2x²―x―1)，(x≥1)，求证：当p≤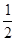－时，有g(x)≤0成立.

（本小题满分12分）

在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图(如图)，已知从左到右各长方形的高的比为2：3：4：6：4：1，第三组的频数为12，请解答下列问题：                                                                                      

(1)本次活动共有多少件作品参加评比？

(2)哪组上交的作品数量最多？共有多少件？

(3)经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率高？

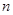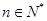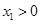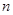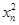（本小题满分12分）自然状态下的鱼类是一种可再生的资源，为了持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响。用表示某鱼群在第年初的总量，，且。不考虑其他因素，设在第年内鱼群的繁殖量及被捕捞量都与成正比，死亡量与成正比，这些比例系数依次为正数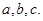其中称为捕捞强度。

（1）求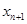与的关系式；

（2）设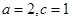，为了保证对任意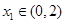，都有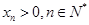，则捕捞强度的最大允许值是多少？证明你的结论。